Understanding Filippov's Inductive Proof for Jordan Canonical Form

Question

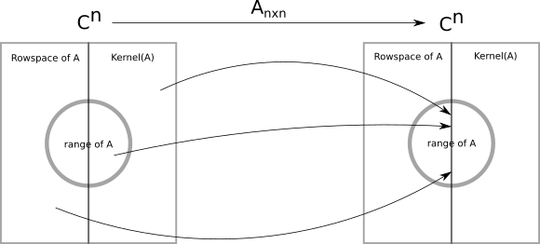
Let $A$ be an $n×n$ complex matrix. Then there exists an invertible matrix $T$ such that $T^{−1}AT=J$ where $J$ is a Jordan form matrix having the eigenvalues of $A$. Equivalently, the columns of $T$ consist of a set of independent vectors $x_1, . . . , x_n$ such that $Ax_k=λ_kx_k$ , or $Ax_k=λ_kx_k+x_{k−1}$.

There exists an inductive proof by Filippov:

1. Base Case ($n = 1$): The Jordan canonical form of the matrix $[a]$ is $[a]$ itself.

2. Inductive Hypothesis: Assume the existence of a Jordan canonical form for all $r \times r$ matrices, $r = 1, 2, \ldots, n-1$, i.e., any $A_{r \times r}$ is similar to a Jordan matrix.

Now consider an $n\times n$ matrix $A$.

Assume $\lambda = 0$ is an eigenvalue, i.e., $A$ is singular. Therefore, the dimension of $C(A)$, the column space of $A$, is $r < n$.

The proof states: "By the induction hypothesis, $A$ (more precisely, the linear operator associated with $A$) restricted to its range has a Jordan canonical form."

What exactly does this statement mean in the context of the induction hypothesis?

My Thoughts:

Thanks to @ancientmathematician for pointing me in the right direction.

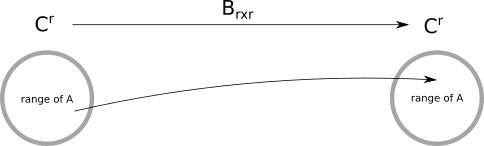
If we think of another tansformation, $T:range(A)\to range(A)$ and the corresponding matrix is $B_{r\times r}$ associated with it, then from the induction hypothesis there exists a Jordan canonical basis $(w_1,\cdots,w_r)$ for the $range(A)$ such that $Bw_k=λ_kw_k$ , or $Bw_k=λ_kw_k+w_{k−1}$.

However, the proof appears to use the same symbol $A$ for both the $n \times n$ matrix and the restricted $r \times r$ matrix $B$, which might be the source of confusion here.

Further Clarification Needed:

Even if that is the case, How can we extend the proof from here and find the conditions for the Jordan basis for the original $n \times n$ matrix $A$ ?

Specifically, how do we transition from: $Bw_k=λ_kw_k$ , or $Bw_k=λ_kw_k+w_{k−1}$. to $Aw_k=λ_kw_k$ , or $Aw_k=λ_kw_k+w_{k−1}$ for the original $n\times n$ matrix $A$ ?

Any insights would be greatly appreciated.

This proof is discussed in A Primer of Abstract Mathematics By Robert B. Ash.

Answer 1

Thanks @ancientmathematician for the hint.

If we think of another transformation, $T:range(A)\to range(A)$ and the corresponding matrix is $B_{r\times r}$ associated with it, ie., $B_{r\times r}$ represents the same $range(A)\to range(A)$ transformations as $A_{n\times n}$, just the space becomes smaller,

then from the induction hypothesis there exists a Jordan canonical basis $(w'_1,\cdots,w'_r)$ for the $range(A)$ such that $Bw'_k=λ_kw'_k$ , or $Bw'_k=λ_kw'_k+w'_{k−1}$.

Step 1

This implies there exists a Jordan canonical basis $(w_1,\cdots,w_r)$ for the $range(A)$ such that $Aw_k=λ_kw_k$ , or $Aw_k=λ_kw_k+w_{k−1}$. The vectors $w_i$ and $w'_i$ are the same except that $w_i$ is a vector in the larger $\mathbb{C}^n$ space and $w'_i$ is the exact same vector represented in the smaller subspace $\mathbb{C}^n$.

Step 2

Let the subspace $N(A)\cap R(A)$ has dimension $p$. The subspace $N(A)\cap R(A)$ is the eigenspace corresponding to the eigenvalue $\lambda=0$. So among the basis vectors $(w_1,\cdots,w_r)$ there are $p$ linearly independent eigenvectors that has eigenvalue $\lambda=0$. Since $w_i\in R(A)$ we have $w_i=Ay_i$ for some $y_i$. Since $Ay_i=0y_i+w_i$ we can place each $y_i$ after each corresponding $w_i$ in the string for all $p$ members in $N(A)\cap R(A)$.

Step 3

Since $dim[N(A)]=n-r$ there are $n-r-p$ vectors $z_i\in N(A)$ that do not belong to $N(A)\cap R(A)$ and $Az_i=0$, ie., there are $n-r-p$ linearly independent eigenvector $z_i\in N(A)$ but not a member of $R(A)$.

Since we have $n$ vectors in $\mathbb{C}^n$ that are in the form $Ax_k=λ_kx_k$ , or $Ax_k=λ_kx_k+x_{k−1}$, we just have to verify the linear independence of $w_i$, $y_i$, $z_i$ to prove the existence of the Jordan canonical basis for any singular square matrix.

Answer 2

This is not an answer to your question. Speaking of an inductive proof, I remember the one by Gelfand, which appeared in the second revised Russian edition (1950) of his textbook Lectures on Linear Algebra and predated Filippov's (1971) proof. The original proof of Gelfand was divided into several steps, but some steps can be merged to make the proof shorter. Below is the shortened proof.

Let $A$ be an $n\times n$ matrix over an algebraically closed field $\mathbb F$. To prove that it is similar to a Jordan form, we use mathematical induction on $n$. The base case $n=1$ is trivial. In the inductive step, pick any left eigenpair $(\lambda,\mathbf z)$ of $A$. By considering $A-\lambda I$ instead of $A$, we may assume that $\lambda=0$. Hence $\mathbf z^\top A=0$ and $S=\{\mathbf x\in\mathbb F^n:\mathbf z^\top\mathbf x=0\}$ is an $(n-1)$-dimensional invariant subspace of $A$. By induction assumption, the restriction of $A$ on $S$ is similar to an upper triangular Jordan form. Therefore we may assume that $A$ takes the form of the block matrix that appears on the LHS of the following equality: $$ \underbrace{\pmatrix{ C&&&&\mathbf u\\ &N_1&&&\mathbf v_1\\ &&\ddots&&\vdots\\ &&&N_k&\mathbf v_k\\ &&&&0}}_{A} \ \underbrace{\pmatrix{ -C^{-1}\mathbf u\\ -N_1^\top\mathbf v_1\\ \vdots\\ -N_k^\top\mathbf v_k\\ 1 }}_{\mathbf x} =\underbrace{\pmatrix{ \mathbf 0\\ \mathbf w_1\\ \vdots\\ \mathbf w_k\\ 0 }}_{\mathbf y}.\tag{1} $$ Here $C$ is a direct sum of nonsingular Jordan blocks and each $N_i$ is a nilpotent Jordan block. With the vector $\mathbf x$ defined in $(1)$, we obtain $$ \mathbf w_i:=-N_iN_i^\top\mathbf v_i+\mathbf v_i=(0,\ldots,0,v_i^{\text{last}})^\top,\tag{2} $$ where $v_i^{\text{last}}$ denotes the last entry of $\mathbf v_i$.

Let $\{\mathbf b_1,\mathbf b_2,\ldots,\mathbf b_n\}$ be the standard basis of $\mathbb F^n$. If $A\mathbf x=0$, we are done because the matrix representation of the linear map $\mathbf t\mapsto A\mathbf t$ with respect to the ordered basis $\{\mathbf b_1,\mathbf b_2,\ldots,\mathbf b_{n-1},\mathbf x\}$ is the Jordan form $C\oplus N_1\oplus\cdots\oplus N_k\oplus0$.

If $A\mathbf x\ne0$, by a suitable permutation we may assume that among all $N_i$s such that $\mathbf w_i\ne0$, $N_k$ has the largest index of nilpotency. Let $N_k$ be $m_k\times m_k$. Denote by $\{\mathbf e_1,\ldots, \mathbf e_{m_k}\}$ the standard basis of $\mathbb F^{m_k}$. Then by $(1)$ and $(2)$, we have $$ A^r\mathbf x =\pmatrix{\mathbf 0\\ N_1^{r-1}\mathbf w_1\\ \vdots\\ N_{k-1}^{r-1}\mathbf w_{k-1}\\ N_k^{r-1}\mathbf w_k\\ 0} =\pmatrix{\mathbf 0\\ \ast\\ \vdots\\ \ast\\ v_k^{\text{last}}\mathbf e_{m_k+1-r}\\ 0}\tag{3} $$ where the first equality is true for every positive integer $r$ and the second one is true when $1\le r\le m_k$. Since $N_k$ has the largest index of nilpotency ($m_k$) among all $N_i$s such that $\mathbf w_i\ne0$, we have $N_i^{m_k}\mathbf w_i=0$ for every $i$. It follows from the first equality in $(3)$ that $A^{m_k+1}\mathbf x=0$ and from the second equality that $\mathcal B=\{\mathbf b_1,\mathbf b_2,\ldots,\mathbf b_{n-(m+1)},A^{m_k}\mathbf x,A^{m_k-1}\mathbf x,\ldots,A\mathbf x,\mathbf x\}$ is a basis of $\mathbb F^n$. Now we are done, because the matrix representation of $\mathbf t\mapsto A\mathbf t$ with respect to $\mathcal B$ is $C\oplus N_1\oplus\cdots\oplus N_{k-1}\oplus J_{m_k+1}(0)$, where $J_{m_k+1}(0)$ denotes a nilpotent Jordan block of size $m_k+1$.