If you have
$h(x) = \frac{4x^2}{x^2-1}$
What is $h(1)$ ? You have something divided by 0 which is undefined.
So 1 cannot be a critical point.
But if you have
$h(x) = |x|$
then $x=0$ is a critical point, because $h(0) = 0$ is well defined and $h'(0)$ is not well defined. So the point is that h is well defined at all critical points. $h'(0)$ can be undefined, but $h(0)$ should be well defined.
Another function:
$f(x) = \begin{cases}
0, & \text{if}\ x=0 \\
\frac{1}{x}, & \text{otherwise}
\end{cases}$
This function is well defined everywhere. But $f'(0)$ is not well defined. So 0 is critical point here.
Another example:
$h(x) = \begin{cases}
0, & \text{if}\ x=1 \\
\frac{4x^2}{x^2-1}, & \text{otherwise}
\end{cases}$
Here 1 is a critical point because now $h(1)$ is well-defined and $h'(1)$ is not well defined. So by making sure the function is defined at 1, we've made it a critical point now.
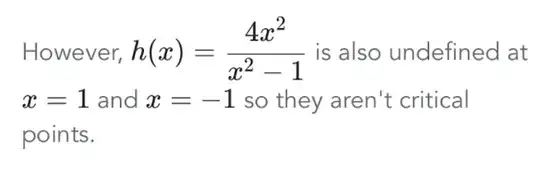
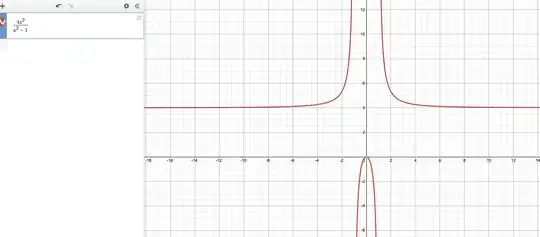
I can see the graphs look different, but.. is that all we are basing it on, we have to draw the graphs to know?
– nvs0000 Nov 14 '20 at 13:06