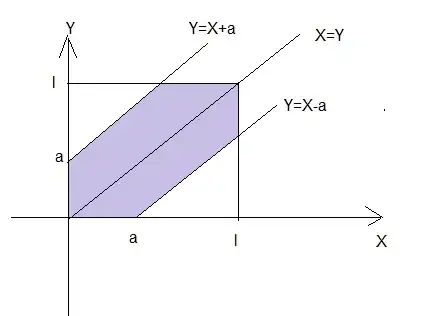
Two individuals agree to meet within the limits of the agreed period $\ l\ $. The first individual to arrive waits for the time $\ a <l$, and then leaves. What is the probability that they will meet?
I tried to use geometric probability.
let Ω = {$(x, y) | 0≤x, y≤ l$}
Using coordinate axes,
Let $(a_1) <(a_2)$ such that $(a_2) - (a_1) = a$
then the area where the coordinate pairs are found should be $[(a_1) ^ 2 - (a_2) ^ 2]$
and the area of Ω = $(l ^ 2)$
So the probability is P (A) = $([(a_1) ^ 2 - (a_2) ^ 2]) / (l ^ 2)$