2

Hello and forgive me for my lack of formality or perhaps poor wording. I am trying to derive the equations for tangent lines common to two Hippopedes ovals with different origins (see Booth's Curve):

$$(x^2+y^2)^2 = a^2x^2 + b^2y^2 $$

and

$$((x-h)^2+(y-k)^2)^2 = a^2(x-h)^2 + b^2(y-k)^2 $$

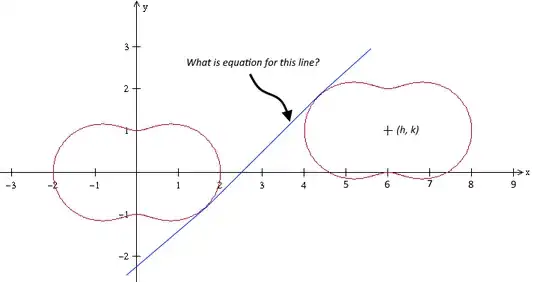
Here is an example:

Example

I believe the solution steps should be something along the lines of:

  1. Find derivatives of each curve ($y'_1$ and $y'_2$)
  2. Set derivatives equal to each other (Eq. 1)
  3. Write slope of line as $y_1-y_0/x_1-x_0$.
  4. Set slope equal to either $y'_1$ or $y'_2$. (Eq. 2)

then solve Eq. 1 and 2 simultaneously. I'm anticipating the math will be cumbersome, so any help would be greatly appreciated! Thank you.

adam.hendry
  • 352
  • Common tangents are parallel to the line connecting $(0,0)$ and $(h,k)$ – Raffaele Oct 28 '20 at 17:27
  • @Raffaele Not necessarily. e.g. If h=10, k=0, you would be right for the two horizontal lines joining the top and bottoms of each curve, but would have missed the other two curves. I will add an illustration to clarify what I am looking for. – adam.hendry Oct 28 '20 at 17:30
  • It's clear. I gave as granted that the curves intersected. Anyway the two other tangents when they don't intersect meet in the midpoint of the two centers – Raffaele Oct 28 '20 at 17:38
  • @Raffaele Would you be able to provide me an example as an answer? – adam.hendry Oct 28 '20 at 17:49
  • Alternatively, I'm wondering if I plug "mx+c" for y in the above and solve that way? – adam.hendry Oct 28 '20 at 17:50
  • https://imgur.com/3TS9sEr – Raffaele Oct 28 '20 at 17:59
  • @Raffaele Did you use Geogebra to solve that? How did you solve that? Also, what proof do you have that the tangent line bisects the line containing the centers? – adam.hendry Oct 28 '20 at 18:00
  • No, I solved nothing. In GeoGebra you can use parametric lines which change as you move a cursor – Raffaele Oct 28 '20 at 18:03
  • Wait! Is this considered a common tangent? https://imgur.com/lDbdvr0 – Raffaele Oct 28 '20 at 18:07
  • @Raffaele No, in regards to your second image, you are okay. I want tangents which intersect each curve at exactly one point. In the second image, the line intersects one of the curves more than once, so it does not count. – adam.hendry Oct 28 '20 at 18:12
  • @Raffaele Thank you for your help as well! I wish I could give you points for credit too! – adam.hendry Oct 28 '20 at 21:25

1 Answers1

1

These ovals have parameterisations

$(x(t),y(t))=(b\frac{ab\cos(t)}{b^2(\cos(t))^2+a^2(\sin(t))^2},a\frac{ab\sin(t)}{b^2(\cos(t))^2+a^2(\sin(t))^2})$ and $(x(t),y(t))=(h+b\frac{ab\cos(t)}{b^2(\cos(t))^2+a^2(\sin(t))^2},k+a\frac{ab\sin(t)}{b^2(\cos(t))^2+a^2(\sin(t))^2}).$

The dual curves are given by $(p(t),q(t))=(\frac{-y'(t)}{x'(t)y(t)-x(t)y'(t)},\frac{x'(t)}{x'(t)y(t)-x(t)y'(t)}).$

Now find the intersection points $P_i$ of the dual curves. Then the common tangents are the lines $x x(P_i)+y y(P_i)=1.$

The picture below shows only a few of the common tangents:

hpct3

Here are the dual curves. Note that they have nodes corresponding to the bitangents.

hpduals

To accentuate the node bitangent correspondence, here are both the curve and its dual, the point and the dual line (bitangent).

hpbitangent

The red intersection point $P_3: (l,m)$ corresponds to the red common tangent through the correspondence $(l:m:-1)$ to $lx +my-1=0.$

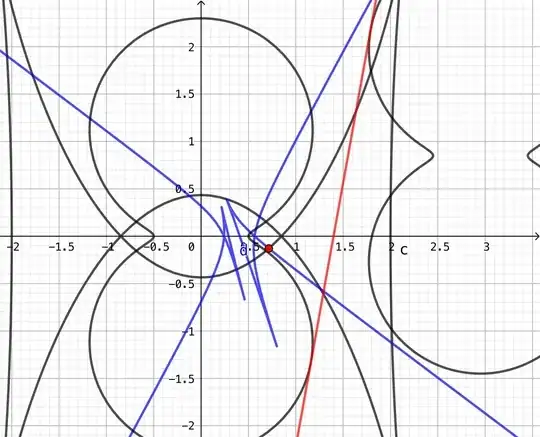
hpintersection

I used $a=0.5, b=2.3, h=2.95, k=0.85$ with the following to get the plot

curve(((a^2*b*sin(t)*(2*a^2*cos(t)*sin(t)-2*b^2*cos(t)*sin(t)))  /(a^2*sin(t)^2+b^2*cos(t)^2)^2  -(a^2*b*cos(t))/(a^2*sin(t)^2+b^2*cos(t)^2))  /((a^2*b*sin(t)        *((-(a*b^2*sin(t))/(a^2*sin(t)^2+b^2*cos(t)^2))         -(a*b^2*cos(t)*(2*a^2*cos(t)*sin(t)-2*b^2*cos(t)*sin(t)))          /(a^2*sin(t)^2+b^2*cos(t)^2)^2))   /(a^2*sin(t)^2+b^2*cos(t)^2)   -(a*b^2*cos(t)      *((a^2*b*cos(t))/(a^2*sin(t)^2+b^2*cos(t)^2)       -(a^2*b*sin(t)*(2*a^2*cos(t)*sin(t)-2*b^2*cos(t)*sin(t)))        /(a^2*sin(t)^2+b^2*cos(t)^2)^2))    /(a^2*sin(t)^2+b^2*cos(t)^2)),((-(a*b^2*sin(t))/(a^2*sin(t)^2+b^2*cos(t)^2))  -(a*b^2*cos(t)*(2*a^2*cos(t)*sin(t)-2*b^2*cos(t)*sin(t)))   /(a^2*sin(t)^2+b^2*cos(t)^2)^2)  /((a^2*b*sin(t)        *((-(a*b^2*sin(t))/(a^2*sin(t)^2+b^2*cos(t)^2))         -(a*b^2*cos(t)*(2*a^2*cos(t)*sin(t)-2*b^2*cos(t)*sin(t)))          /(a^2*sin(t)^2+b^2*cos(t)^2)^2))   /(a^2*sin(t)^2+b^2*cos(t)^2)   -(a*b^2*cos(t)      *((a^2*b*cos(t))/(a^2*sin(t)^2+b^2*cos(t)^2)       -(a^2*b*sin(t)*(2*a^2*cos(t)*sin(t)-2*b^2*cos(t)*sin(t)))        /(a^2*sin(t)^2+b^2*cos(t)^2)^2))    /(a^2*sin(t)^2+b^2*cos(t)^2)),t,0,2pi)
curve(((a^2*b*sin(t)*(2*a^2*cos(t)*sin(t)-2*b^2*cos(t)*sin(t)))  /(a^2*sin(t)^2+b^2*cos(t)^2)^2  -(a^2*b*cos(t))/(a^2*sin(t)^2+b^2*cos(t)^2))  /(((a^2*b*sin(t))/(a^2*sin(t)^2+b^2*cos(t)^2)+k)   *((-(a*b^2*sin(t))/(a^2*sin(t)^2+b^2*cos(t)^2))    -(a*b^2*cos(t)*(2*a^2*cos(t)*sin(t)-2*b^2*cos(t)*sin(t)))     /(a^2*sin(t)^2+b^2*cos(t)^2)^2)   -((a^2*b*cos(t))/(a^2*sin(t)^2+b^2*cos(t)^2)    -(a^2*b*sin(t)*(2*a^2*cos(t)*sin(t)-2*b^2*cos(t)*sin(t)))     /(a^2*sin(t)^2+b^2*cos(t)^2)^2)    *((a*b^2*cos(t))/(a^2*sin(t)^2+b^2*cos(t)^2)+h)), ((-(a*b^2*sin(t))/(a^2*sin(t)^2+b^2*cos(t)^2))  -(a*b^2*cos(t)*(2*a^2*cos(t)*sin(t)-2*b^2*cos(t)*sin(t)))   /(a^2*sin(t)^2+b^2*cos(t)^2)^2)  /(((a^2*b*sin(t))/(a^2*sin(t)^2+b^2*cos(t)^2)+k)   *((-(a*b^2*sin(t))/(a^2*sin(t)^2+b^2*cos(t)^2))    -(a*b^2*cos(t)*(2*a^2*cos(t)*sin(t)-2*b^2*cos(t)*sin(t)))     /(a^2*sin(t)^2+b^2*cos(t)^2)^2)   -((a^2*b*cos(t))/(a^2*sin(t)^2+b^2*cos(t)^2)    -(a^2*b*sin(t)*(2*a^2*cos(t)*sin(t)-2*b^2*cos(t)*sin(t)))     /(a^2*sin(t)^2+b^2*cos(t)^2)^2)    *((a*b^2*cos(t))/(a^2*sin(t)^2+b^2*cos(t)^2)+h)),t,0,2pi)

There are ways to get the implicit equations defining the dual curves (I'd need to read up on them), and you could further use grobner bases.

The first has equation $a^4b^{10}x^6+3a^6b^8x^4y^2+3a^8b^6x^2y^4+a^{10}b^4y^6+(8a^6b^6-8a^4b^8-a^2b^{10})x^4+(-20a^8b^4+38a^6b^6-20a^4b^8)x^2y^2+(-a^{10}b^2-8a^8b^4+8a^6b^6)y^4+(16a^8b^2-32a^6b^4+8a^4b^6+8a^2b^8)x^2+(8a^8b^2+8a^6b^4-32a^4b^6+16a^2b^8)y^2-16a^6b^2+32a^4b^4-16a^2b^6=0$

Jan-Magnus Økland
  • 6,019
  • Okland Can you go into a little more detail about how to calculate the intersection points themselves? – adam.hendry Oct 28 '20 at 18:49
  • @A.Hendry I used the intersect command in geogebra. – Jan-Magnus Økland Oct 28 '20 at 18:51
  • 1
    @Jan-Magnus_Okland I'm not sure I understand the dual curves image you posted. – adam.hendry Oct 28 '20 at 19:02
  • Without using geogebra, how would you calculate the intersection points? (I'm trying to derive general equations) – adam.hendry Oct 28 '20 at 19:03
  • Would Mathematica or a similar solver be necessary to get general equations for these intersection points? – adam.hendry Oct 28 '20 at 19:09
  • In the above, when you use $xx(P_i) + yy(P_i) = 1$, are these in line coordinates? (i.e. $lx + my + 1 = 0$)? – adam.hendry Oct 28 '20 at 19:40
  • More like $l x+m y-1=0,$ where $l=x(P_i),m=y(P_i).$ – Jan-Magnus Økland Oct 28 '20 at 19:42
  • I see. Thank you. These are several new concepts for me and I appreciate your help. So there are two dual curves (black is for the Hippopedes oval at origin, blue for the translated $(h,k)$ one). The intersection points between the black and blue curves yield the $P_i$ for the common tangent lines. Is that correct? Can you also show me on your graphs the nodes you speak of that correspond to the bitangents? – adam.hendry Oct 28 '20 at 19:51
  • @A.Hendry See the edit. – Jan-Magnus Økland Oct 28 '20 at 20:00
  • Instead, can you show me the nodes for the bitangents across each curve, not across an individual curve? Those are the ones I'm interested in, sorry. Is there a way to know which nodes lead to the types of bitangents that occur? – adam.hendry Oct 28 '20 at 20:23
  • That’s what bitangents are. Common tangents correspond in the same way though. – Jan-Magnus Økland Oct 28 '20 at 20:27
  • Oh, forgive me. I didn't know the difference between bitangent and common tangent. I meant common tangent. I apologize. Can you show me a node for a common tangent? – adam.hendry Oct 28 '20 at 20:30
  • And $P_i$ is a parameter like $t$, not an $(x, y)$ point, right? – adam.hendry Oct 28 '20 at 20:35
  • $P_i$ is a point. – Jan-Magnus Økland Oct 28 '20 at 20:36
  • I see now! Thank you so much! – adam.hendry Oct 28 '20 at 20:41
  • $P_3: (0.71,-0.13)$ corresponding to $0.71 x-0.13 y-1=0.$ – Jan-Magnus Økland Oct 28 '20 at 20:41
  • Yes, you're right. I deleted the comment I previously made regarding the bitangent node as I was wrong (it is $~(-0.42,0)$, not $~(0,-0.42)$). And thank you for all your help! I totally get it now! – adam.hendry Oct 28 '20 at 20:46
  • For posterity: As @Jan-MagnusOkland beautifully states, $P_i = (l_i, m_i)$ and $l_i$ and $m_i$ are the negative reciprocals of the $x$ and $y$ intercepts for the tangent line (https://en.wikipedia.org/wiki/Line_coordinates). So, if you know roughly where these intercepts will be for your desired line, you can search the space of intersection points correspondingly to find your line! Brilliant! – adam.hendry Oct 28 '20 at 20:52