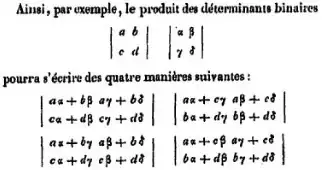1

Seeing that a lot of linear algebra is based on matrices and operations on that representation, I wonder at which point came the notion of transposition of a linear map (LM) (or matrix as well). Both definitions seem very different and the linear map one seems a lot more convoluted with all those details on isomorphisms of dual spaces <-> vector spaces and etc... almost like someone tried very hard for both matrix and LM transposes to type the same.

If the answer to that question is that LM transpose notion came first then it seems more natural to have a notion on matrix transposition as we do now however, I only knew about matrix transposition and I'm not aware of any uses of LM transposition that justify the ubiquity of matrix transposition. It seems like an interesting coincidence following this line of reasoning.

If the answer to that question is that matrix transpose notion came first then it suggests that the "Dual Space" notion was developed/created/discovered as a way to enrich the theory with a way for transposition to work/make sense in terms of linear maps. I say this because, from what I know, only vector spaces have this notion and it seems to have some sort of a more general context waiting to be explored!

Does anyone have any scientific evidence that can answer the question? I'd also appreciate if you could educate me and correct my understanding about this topic or my line of reasoning.

bolt12
  • 11

2 Answers2

3

These concepts applied to matrices have been developed rather later, in the early 1920s/1930s (see below). They were almost unknown in the 19th century, even if matrices were invented at that time.

In fact, matrices were completely shadowed by determinants: the transpose, products, etc. of determinants predated for a long time similar operations on matrices.

Here is for example a short excerpt

enter image description here

from "Théorie des déterminants et leurs principales applications" (Francesco Brioschi) in its French translation (1856) availaible on the site gallica.bnf.fr showing that people at that time had a good working knowledge of equivalents of $\det(AB)=\det(AB^T)=\det(A)\det(B)$ involving products and transpositions, in the perspective of techniques, computational rules that were not based on a theoretical vision.

Here is an excerpt of 1923 lecture notes by Hermann Weyl: "$\overline{A}$ bedeutet die durch Vertauschung der Zeilen und Kolonnen aus $A$ entstehende "transponierte" Matrix" (transl. : $\overline{A}$ designates the "transposed" matrix resulting from the exchange of rows and columns of $A$). Reference "L'analyse mathématique du problème de l'espace", Hermann Weyl, Editor: Episteme, Presses Universitaires de Provence, 2015, bilingual edition.

Jean Marie
  • 88,997
  • I see, thanks for your answer! Just to clarify are you saying that matrices came first, as well as techniques/computational rules that were not based on a theoretical vision? – bolt12 Oct 25 '20 at 14:17
  • Yes, more exactly, determinants came first, then matrices have been deeply used (and I would say understood) in the 1920s (in particular with quantum mechanics and Schrödinger) under the impulsion of "new wave" (mainly german) mathematicians of the "Hilbert school" like Hermann Weyl together with their generalization, tensor calculus; this has paved the way to the abstract point of view that emerged around 1940-1950 (Artin, Bourbaki,...) – Jean Marie Oct 25 '20 at 14:36
  • I see, thanks! So what are your opinions on the dual space notion, do any of my lines of reasoning are pertinent? – bolt12 Oct 25 '20 at 15:28
  • It is worth knowing that duality has a long history with deep geometrical sources, in particular with the duality point-line with respect to a conical curve (discovered in the early 1820s). Here are some references collected from some of my answers on this site. A geometrical reason explained on the particular case of a circle: (https://math.stackexchange.com/q/3873446) and an anlytical reason ((https://math.stackexchange.com/q/3842796) ). See as well: (https://math.stackexchange.com/q/2004994). Of course, much more could be said... – Jean Marie Oct 25 '20 at 15:54
  • Connected: https://math.stackexchange.com/q/3749 – Jean Marie Oct 25 '20 at 20:00
2

It seems you've encountered a particularly ugly definition of the transpose of a linear map. If $T:V\to W$ is a linear map of vector spaces, then its transpose is the linear map $T^*:W^*\to V^*$ defined by $T^*(f)=f\circ T$. It's just composition of linear maps, and it doesn't need any isomorphisms, inner products, etc.

As for your historical question, I'd guess that almost everything was done with matrices, in the 19th century, before linear transformations were developed and simplified these things.

Andreas Blass
  • 75,557
  • Thanks for your answer! I must clarify about " linear map one seems a lot more convoluted ....". I am aware of that definition. What I think it's convoluted is the fact that for defining the transpose of a LM you have to have a notion of dual space which from my understanding is unique to vector spaces and feel non-intuitive when compared to the matrix counterpart. If we look to the types of both LM and Matrix transpose we see that they are different since the former involves Dual S, but interestingly enough its possible to recover the same type as the matrix transpose by going via isomorphism – bolt12 Oct 25 '20 at 14:14