2

Show that the distance between parallel planes, $ax + by + cz + d_1 = 0$, and $ax + by + cz + d_2 = 0$ is,

$$ D = \frac{|d_1-d_2|}{\sqrt{a^2+b^2+c^2}} $$

Solution:

(a) Get the distance from point (x, y, z) to the plane, $ax+by+cz+d_1 = 0$.

$$ D = \frac{|ax+by+cz +d_1|}{\sqrt{a^2+b^2+c^2}} $$

(b) Get the value of ax + by + cz.

  • $d_1 = d_2$ since $-d_1 = ax+by+cz$, and $-d_2 = ax+by+cz.$

(c) Substitute ax+by+cz into $-d_2$, since, $-d_2 = ax+by+cz$

$$ D= \frac{|ax+by+cz +d_1|}{\sqrt{a^2+b^2+c^2}} $$ $$ D= \frac{|d_1 - d_2|}{\sqrt{a^2+b^2+c^2}} $$

QED
Clemens Bartholdy
  • 14,222
Cyrus
  • 45

1 Answers1

1

$"d_1=d_2$ since$ −d_1=ax+by+cz$, and $−d_2=ax+by+cz."$

This is clearly wrong. Since the planes are parallel, by definition there is no $ (x,y,z)$ triplet which satisfies both conditions at once.

Proof sketch:

  1. Draw the two parallel planes! (let's call the two planes $\pi_1$ and $\pi_2$)
  2. Pick one point on each plane, construct a vector from these two points [ assume coordinates of the point]
  3. Dot this vector with the normal of the plane [ why? look at the picture!]

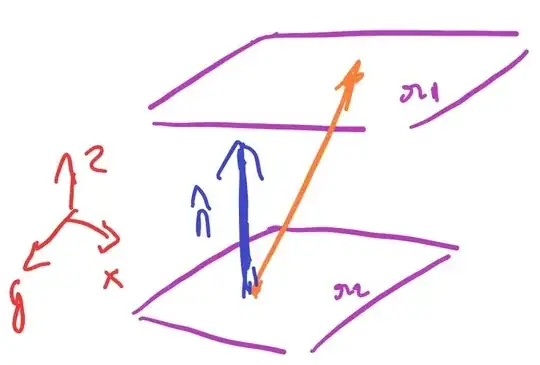
enter image description here

Legend:

  • orange vector is the one connecting the point on each of the parallel planes
  • Blue is the normal (same for both planes)

The general solution:

Assume two points $(x_1,y_1,z_1)$ and $(x_2,y_2,z_2)$ then the vector connecting them is:

$$ \vec{r} = (x_2 - x_1, y_2 - y_1 , z_2 - z_1)$$

Now notice the equation in G Cab's comment:

$$ a(x_2 - x_1) + b(y_2 - y_1) + c(z_2 - z_1) = d_2 - d_1$$

We can write this as:

$$ \begin{bmatrix} a \\ b \\ c \end{bmatrix} \cdot \begin{bmatrix} x_2 - x_1 \\ y_2 - y_1 \\ z_2 - z_1 \end{bmatrix} = d_2 - d_1$$

Now normalize the unit vector :

$$ \frac{1}{\sqrt{a^2 + b^2 +c^2} } \begin{bmatrix} a \\ b \\ c \end{bmatrix} \cdot \begin{bmatrix} x_2 - x_1 \\ y_2 - y_1 \\ z_2 - z_1 \end{bmatrix}= \frac{d_2 - d_1}{\sqrt{a^2 + b^2 +c^2} }$$

This quantity can be geometrically interpreted as the distance the perpendicular distance between two planes and hence:

$$ D= = \frac{d_2 - d_1}{\sqrt{a^2 + b^2 +c^2} }$$

You can take modulus on both sides but actually, the sign has meaning as is discussed in this stack post

Clemens Bartholdy
  • 14,222
  • Thank you for answering. I also feel it is wrong. – Cyrus Oct 20 '20 at 17:52
  • Do you wish for help on the correct way to proceed? – Clemens Bartholdy Oct 20 '20 at 17:53
  • Yes, that would be a great help. – Cyrus Oct 20 '20 at 17:53
  • 2
    well, of course there is no triplet satisfying both equations : the planes are parallel. what we have to find is their distance – G Cab Oct 20 '20 at 17:57
  • I have added a picture and written a proof sketch, I suggest you try it yourself. If you don't get it then don't hesitate to ask for hints – Clemens Bartholdy Oct 20 '20 at 17:58
  • Thank you so much! I will try answering it myself. – Cyrus Oct 20 '20 at 18:00
  • The vector is <[(d2-d1)/a],0,0>, and normal is <a,b,c>, right? After that, I just have to get the scalar of the projection of the vector onto the normal vector right? – Cyrus Oct 20 '20 at 18:20
  • How did you conclude that the vector would be $ \frac{d_2 - d_1}{a} $? I suggest taking the most general choice of $ (x_1, y_1 , z_1)$ and $ (x_2 , y_2 , z_2)$ as the point on each plane – Clemens Bartholdy Oct 20 '20 at 18:32
  • And yep dot it onto the ** unit normal** and use the equations of plane to simplify the expression – Clemens Bartholdy Oct 20 '20 at 18:33
  • I concluded that the vector would be, $\frac{d_1 - d_2}{a}$ rather by substituting y and z to 0 in both planes to get the value of x and uses these points, $(-\frac{d_2}{a},0,0)$ and $(-\frac{d_1}{a},0,0)$, as the initial and terminal points for the vector. – Cyrus Oct 20 '20 at 18:44
  • Actually, that should work. That should solve the problem, I had the idea in my head to do with most general points but even those two specific points will do :) – Clemens Bartholdy Oct 20 '20 at 18:48
  • Thank you for the help! I really appreciate it. – Cyrus Oct 20 '20 at 18:55
  • I've added a general solution, if this answer was helpful then you can accept it. – Clemens Bartholdy Oct 20 '20 at 19:02