Rank of a $n! \times n$ matrix

Question

This question is about showing that $n!$ points resulting from applying a function (defined below) to the permutations of $n$ numbers lie on a $n-1$ dimensional hyperplane.

Let $X=\langle x_1,\cdots,x_n \rangle$ and $Y=\langle y_1,\cdots,y_n \rangle$ be vectors of positive reals and let $P=\langle p_1,\cdots,p_n \rangle$ be a permutation of the numbers $\{1,\cdots,n\}$. Let,

$$ y_i=\log\left(1+\frac{x_i}{1+\sum\limits_{p_j<\,p_i}x_j}\right) $$ be a mapping from $X,P$ to $Y$. So, for any given vector $X$, we have $n!$ (one for each permutation) output vectors $Y$. Let $Y_P$ denote a vector resulting from permutation $P$. Now, for a given $X$, create a matrix $M$ such that each row of it is $Y_P-Y_{P_1}$ for a fixed $P_1$ and for all $P$.

$$ M=\begin{bmatrix} Y_{P_1}-Y_{P_1} \\ Y_{P_2}-Y_{P_1} \\ \vdots \\ Y_{P_{n!}}-Y_{P_1} \end{bmatrix} $$

So, $M$ is a $n! \times n$ matrix. I have two questions:

1. I guess the rank of $M$ is at most $n-1$, that is all of $Y$'s lie on a hyperplane of dimension $n-1$ (I verified it for $n=3$ and $n=4$). Is that true or not? Why?
2. For what sort of mappings from $X,P$ to $Y$, is the answer to the previous question positive?

Edit 3:

I realized that for all of the permutations, $\sum_i y_i = \log(1+\sum_i x_i)$ and as Chris Culter commented below, this might be the solution to the problem. The proof of inequality is long but an example clears its correctness: consider $n=3$ and $P=\langle 1, 2, 3 \rangle$,

$$ \begin{align} y_1+y_2+y_3&= \log(1+\frac{x_1}{1+x_2+x_3})+ \log(1+\frac{x_2}{1+x_3})+ \log(1+\frac{x_3}{1})\\ &= \log(\frac{1+x_1+x_2+x_3}{1+x_2+x_3})+ \log(\frac{1+x_2+x_3}{1+x_3})+ \log(\frac{1+x_3}{1})\\ &= \log(1+x_1+x_2+x_3). \end{align} $$

Since any other permutation only renames $x_1$, $x_2$, and $x_3$, the output remains the same.

Edit 2:

The problem has a specific structure which may help solving it: The $n!$ points consist of $n$ ensembles of $(n-1)!$ points. Ensemble $i$ consists of all of the points $Y_P$ such that $i^{th}$ element of $P$ is 1. Therefore, all of the points in ensemble $i$ has the same $y_i$.

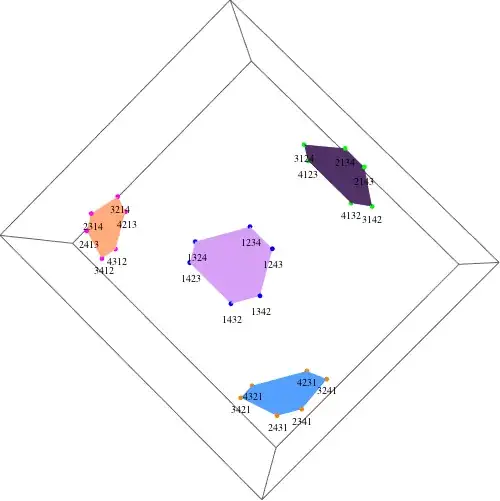
For example, for $n=3$, there are 3 ensembles of 2 points (6 points in total). All of the points lie on a 2D plane. The following figure shows an example in 3D:

Points in the same ensemble have a same colour. The labels beside the points denote the permutation that generates the point. So, points 123 and 132 are in ensemble 1, points 213 and 312 are in ensemble 2 (1 is the second element of their permutation), and points 231 and 321 are in ensemble 3 (1 is the third element of their permutation).

For $n=4$, there are 4 ensembles of 6 points (24 points in total). Since all of the points in 4D lie on a 3D plane, we can project the points into the 3D space. Here is an example:

Higher dimensions are recursively constructed as described above. So, for $n=5$, there are 5 ensembles of the form shown above (in 4D). This recursive nature can be useful for solving the problem.

Edit 3:

• I used Mathematica to verify my conjecture for $n=3$ to $8$ and it's correct. See my other question on Mathematica.SE. For $n>8$, because of the exponential running time of the algorithm, it's hard to verify the conjecture.

• The above conjecture also holds for the following mapping functions:

$$ y_i={x_i}-{\sum\limits_{p_j<\,p_i}x_j} $$

$$ y_i={x_i}^3-{\sum\limits_{p_j<\,p_i}{x_j}^2} $$

• But it does not hold for the following functions:

$$ y_i=\log\left(\frac{x_i}{1+\sum\limits_{p_j<\,p_i}x_j}\right) $$

$$ y_i={x_i}^3-\left(\sum\limits_{p_j<\,p_i}x_j\right)^2 $$

Answer 1

Answer to the first question As Chris Culter guessed, the answer is YES and this is because $\sum_{i}y_i=\ln(1+\sum_{i} x_i)$. The proof of this last identity is not difficult, it is basically a change of indices and a careful use of notation (see below). What you have here is a telescoping sum (or product, depending on the way in which you look at it), but disposed according to a random order (depending on the permutation $p$).

$$ \begin{array}{lcl} e^{\prod_{i=1}^n y_i} &=&\prod_{i=1}^n e^{y_i} \\ &=& \prod_{i=1}^n \frac{1+x_i+\sum_{p(j)<p(i)}x_j}{1+\sum_{p(j)<p(i)}x_j} \\ &=& \prod_{I=1}^n \frac{1+x_{p^{-1}(I)}+\sum_{J<I}x_{p^{-1}(J)}} {1+\sum_{J<I}x_{p^{-1}(J)}} \ \text{(where we put } I=p(i),J=p(j) \text{)} \\ &=& \prod_{I=1}^n \frac{1+z_I+\sum_{J=1}^{I-1}z_J} {1+\sum_{J=1}^{I-1}z_J} \ \text{(where we put } z_I=x_{p^{-1}(I)} \text{)} \\ &=& \prod_{I=1}^n \frac{t_I} {t_{I-1}} \ \text{(where we put } t_I=1+\sum_{J=1}^{I}z_J \text{)} \\ &=& \frac{t_N} {t_0}=1+x_1+x_2+\ldots +x_n. \end{array} $$

Partial answer to the second question

When $y_i$ is of the form $A(x_i)-\sum_{p(j)<p(i)}B(x_j)$ where $A$ and $B$ are functions, your conjecture still holds, because

$$ \sum_{i}B(x_i)y_i=\sum_{i}A(x_i)B(x_i)-\frac{1}{2}\sum_{I\neq J}B(x_I)B(x_J) $$

When $A(x)=x$ and $B(x)=x$, you get $y_i=x_i-\sum_{p(j)<p(i)}x_j$.

When $A(x)=x^3$ and $B(x)=x^2$, you get $y_i=x_i^3-\sum_{p(j)<p(i)}x_j$.