One helpful hint is that if you find a solution, then the matrix obtained by negating a row is still a solution. Another hint: if you regard a column and its negation as an equivalence class, how many classes are there? How many of these must actually get used? What can you say about classes that don't get used? How does this relate to the hint about row negations?
The key hint for this problem, however, is contained in the original problem statement. It's the question whether the solution can be generalized. I would recommend trying generalizations with shorter columns, say columns of length $2$ or $3,$ before trying generalizations with longer columns, and even before attempting to construct the $4\times39$ example. You will have to figure out what the row length will be in the general case, using considerations like the ones above. Once you have that, it should be possible to do the smallest-size cases by exhaustive search. Can you build on these results to construct larger examples?
Added: To be clear, my hints were suggesting a recursive construction. To answer the questions raised in my first paragraph: for columns of length $\ell,$ there are $\frac{1}{2}(3^\ell-1)$ classes. When $\ell$ is $4,$ that means $40$ classes. So if we are to have 39 columns, then one class will be unused. This suggests a possible generalization to $\ell\ne4$, and we let
$$s(\ell)=\frac{1}{3}\left[\frac{1}{2}(3^\ell-1)-1\right]=\frac{1}{6}(3^\ell-3),$$
which is an integer. We look for matrices of $\ell$ rows and $3s(\ell)$ columns satisfying your conditions (1), (2), and (3), and having $s(\ell)$ each of $1,$ $0,$ and $-1$ in every row.
Since the two members of each equivalence class differ only in sign, the number and positions of zeros are independent of which member is chosen to represent the class. There are $3^\ell$ vectors of length $\ell$ with elements in $\{-1,0,1\},$ comprising $\ell\cdot3^\ell$ total elements, of which a third, or $\ell\cdot3^{\ell-1},$ are zero. Since the zero vector, containing $\ell$ zeroes, is not to be used, any set constisting of one representative of each equivalence class contains $\frac{1}{2}(\ell\cdot3^{\ell-1}-\ell)=\frac{1}{6}(3^\ell-3)\ell=s(\ell)\ell$ zero elements. This is exactly the number of zero elements needed to satisfy condition (4) on row elements, which implies that all of the equivalence classes containing zero elements get used. So one of the equivalence classes containing only $\pm1$ elements is the unused class. Since the row normalization is arbitrary, we can take the missing class to be the class consisting of the all-ones vector and its negation.
Let us solve the $\ell=2$ case first. We have $s(\ell)=1.$ The columns will be $\pm(1,0)^T,$ $\pm(0,1)^T,$ and $\pm(1,-1)^T.$ If we choose the signs $+,$ $-,$ and $-,$ we get the matrix
$$M_2=\begin{bmatrix}1 & 0 & -1\\0 & -1 & 1\end{bmatrix},$$
which has one $1,$ one $0,$ and one $-1$ in each row.
If we have constructed a matrix $M_\ell,$ satisfying conditions (1), (2), and (3), and having $s(\ell)$ $1\text{s,}$ $s(\ell)$ $0\text{s,}$ and $s(\ell)$ $-1\text{s}$ in each row, then the $\ell\times9s(\ell)$ matrix
$$\begin{bmatrix}M_\ell & M_\ell & M_\ell\end{bmatrix}$$
has $3s(\ell)$ $1\text{s,}$ $3s(\ell)$ $0\text{s,}$ and $3s(\ell)$ $-1\text{s}$ in each row. Of course we now have three copies of each column, but by prefixing each copy with a different element, $1,$ $0,$ or $-1,$ we obtain an $(\ell+1)\times9s(\ell)$ matrix with distinct columns and $3s(\ell)$ $1\text{s,}$ $3s(\ell)$ $0\text{s,}$ and $3s(\ell)$ $-1\text{s}$ in each row. Since $s(\ell+1)=3s(\ell)+1,$ to construct $M_{\ell+1}$ we need one additional $1,$ $0,$ and $-1$ in each row. A construction of $M_{\ell+1}$ can be achieved as follows:
$$M_{\ell+1}=\left[\begin{array}{c|ccc|c|ccc|c|ccc}1 & 1 & \ldots & 1 & 0 & 0 & \ldots & 0 & -1 & -1 & \ldots & -1\\
\hline
0 & & & & -1 & & & & 1 & & & \\
\vdots & & M_\ell & & \vdots & & M_\ell & & \vdots & & M_\ell & \\
0 & & & & -1 & & & & 1 & & &
\end{array}\right].$$
Since $M_\ell$ does not contain the all-zero column, the all-one column, or the all-minus-one column, neither does $M_{\ell+1}.$ Since $M_\ell$ contains neither duplicate columns, nor columns which are negations of each other, neither does $M_{\ell+1}.$ All conditions are therefore satisfied. Here's an image:

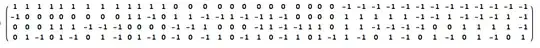


 (This probably does not generalize easily though.)
(This probably does not generalize easily though.)