3

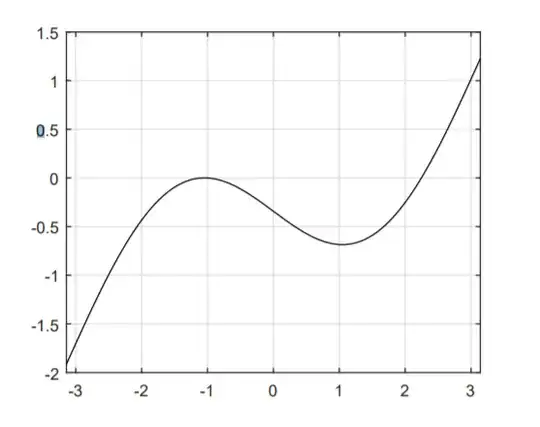
Suppose we wish to compute the zeros of the function $f(x) = \frac{x}{2} - \sin x + \frac{\pi}{6} - \frac{\sqrt{3}}{2}=0$, which has exactly two roots in the interval $[-\pi,\pi]$.

Is it possible to apply the bisection method to compute both roots? Why? For the root(s) which can be found by bisection, estimate the number of iterations necessary to compute the root(s) to a relative accuracy tol = $10^{-10}$, having chosen a suitable starting interval.

I'm guessing that for the first part of the question I have to use the conditions for the bisection method (that $f$ has to be continuous on an interval $[a,b]$ and that $f(a)f(b) \leq0$) and check if both roots satisfy them or not (obviously one of the roots satisfies them and the other does not) but I'm not sure how to write this out formally.

So for the first root, it lies in the interval [-2,0] while the second root lies in the interval [2,3]. I can see that for the first root f(-2)<0 and f(0)<0 which means that f(-2)f(0)>0 and so it does not satisfy the condition for the bisection method. Is this sufficient in answering the first part of the question?

The graph of the function

user839136
  • 51
  • 2
    Welcome to MSE! This sounds like you are assigning us homework, which will lead to question closure. To avoid this, add context such as what you've tried, where you got stuck, graphs of the function, where this problem came from, etc. For more details see the help center and How to ask a good question. – Simply Beautiful Art Oct 19 '20 at 13:12
  • To use bisection to find two roots, you will need to find two intervals that each contain only one of the roots. Otherwise, bisection will converge to one and you won't find the other. One way to do that is to find an interval where $f(c)$ has one sign, $f(d)$ has the other sign, and $f'(x)$ has one sign on $[c,d]$, so that you can be sure that there is only one root in $[c,d]$. – Ian Oct 19 '20 at 13:28
  • 1
    So for the first root, it lies in the interval [-2,0] while the second root lies in the interval [2,3]. I can see that for the first root f(-2)<0 and f(0)<0 which means that f(-2)f(0)>0 and so it does not satisfy the condition for the bisection method. Is this sufficient in answering the first part of the question? – user839136 Oct 19 '20 at 13:30
  • 1
    I guess you are asking about the technicality of the double root? You are correct that there is no bracket of the left root with different signs on either end. The specific bracket $[-2,0]$ does not really prove that, but a graph would. Some playing around with derivatives would, too. – Ian Oct 19 '20 at 13:33
  • If the graph was provided with the question (as above) then would it be sufficient to talk about the specific bracket [-2,0]? – user839136 Oct 19 '20 at 14:58
  • Pedantically speaking, no. Think about a continuous function with $f(0)=-1,f(1)=0,f(2)=1,f(3)=-1$. $[0,3]$ is a bracket of 1 but it doesn't have the desired sign property. But $[0,2]$ is another bracket of $1$ which does have the desired sign property. If you're going to be pedantic, you would need to say that any interval containing the left root and a point with a positive function value will also have to contain the right root. That can (more or less) be seen from the graph (though to really prove it you would need to already know analytically what the left root is). – Ian Oct 19 '20 at 17:04
  • To put it a different way, bisection doesn't really find roots. It finds sign changes. For continuous functions, sign changes happen at roots, but not every root has an associated sign change. – Ian Oct 20 '20 at 22:43

1 Answers1

1

As mentioned in the comments, checking $[-2,0]$ is not enough to say bisection cannot be used to find the left root. Are there points closer to the root where $f$ changes sign? Graphically, you could say this is not the case.

To show $f$ never changes signs, you want to show that its maximum is $0$. This local maximum can be found by finding the root of the derivative (in fact the bracket $[-2,0]$ will work for this). A number of technical details are needed, but you can also show this is the only local maxima for $x\le0$. If the local maximum is found analytically, then you have a formal proof that $f(x)\le0$. If you use a root-finding or optimization algorithm to find the local maximum, then you have a heuristic that $f(x)\le0$.

Simply Beautiful Art
  • 76,603