0

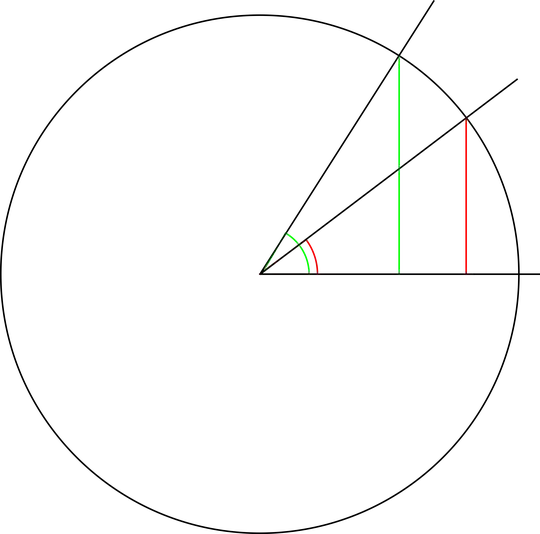
In an acute triangle, if $\measuredangle A > \measuredangle B$, then $\sin\measuredangle A > \sin\measuredangle B$. Why is this true?

Mohsen Shahriari
  • 7,071
Mahdi Rkioui
  • 508
  • 1
    See https://www.mathopenref.com/triggraphsine.html as discussed at https://math.stackexchange.com/questions/3851112/what-is-the-physical-meaning-of-sine-cosine-and-tangent-of-an-obtuse-angle/3851143#3851143 – user2661923 Oct 18 '20 at 09:10

3 Answers3

2

Depending on how you define sine, this picture may already help you through:

enter image description here

Hagen von Eitzen
  • 382,479
  • Right now I'm only thinking of it in terms of the ratios, sin = opposite / hypotenuse, I'm not very familiar with the unit circle definition. – Mahdi Rkioui Oct 18 '20 at 09:06
2

The result follows because $0 \leq A < B \leq \frac{\pi}{2}$, and $\sin$ is a strictly increasing function on $[0, \frac{\pi}{2}]$. The latter can be shown from the definition of $\sin$ and Pythagoras's theorem, or some calculus.

DavidW
  • 572
1

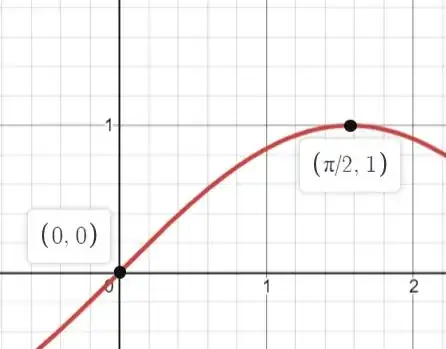
By definition, all angles in an acute triangle are less than 90 degrees. Therefore, from the graph of $\displaystyle \sin( x)$, we know that it is an increasing function on the interval $\displaystyle \left[ 0,\frac{\pi }{2}\right]$. enter image description here

Therefore, as $\displaystyle \sin( x)$ is an increasing function, if $\displaystyle a\ >b$, then $\displaystyle \sin( a) >\sin( b)$.

Omar hatem
  • 24