Geometric Similarity of Functions

Question

I am a 16 year old high school student and recently I have written a paper on a numerical approximation of distinct functions. I have shown my teachers this and they do not understand it. My questions: Is this a valid theorem to use to estimate functions with differently based functions? Has something similar already been created? Is it all useful/publishable? Any tips on how to improve? I will give an outline but you can find it here: https://www.overleaf.com/read/xjqhfgvrcrbj

Definitions

Geometric similarity refers to the dilation of a particular shape in all its dimensions. Proofs of geometric similarity are included in congruence proofs of triangles with AAA (Angle-Angle-Angle) proofs. Knowing the sizes of all sides of both triangles: $\triangle{ABC}$ and $\triangle{A'B'C'}$, to find the dilation factor and prove geometric similarity the following must be true: $\frac{\mid A' \mid}{\mid A \mid} =\frac{\mid B' \mid}{\mid B \mid}=\frac{\mid C' \mid}{\mid C \mid}$.

Interpreting functions as shapes on the Cartesian plane and using geometry, geometrically similar functions can be calculated. Analytically this would imply for a function $y=f(x)\; \{x_0\leq x \leq x_1\}$ a geometrically similar function would be of the form $ny=f(nx)\;\{\frac{x_0}{n}\leq x \leq \frac{x_1}{n}\}$ where $n\in {\rm I\!R}$. This is because the function is scaled by the same factor in the $x$ and $y$ direction thus would be geometrically similar.

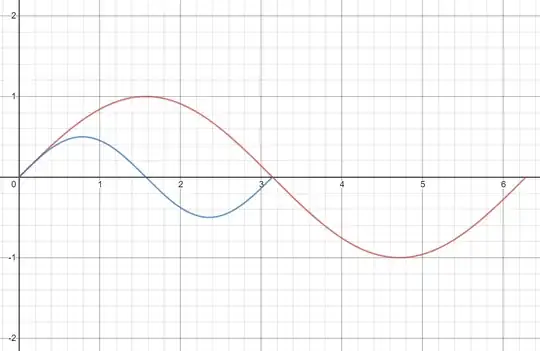$y_1=\sin(x)\;\{0\leq x \leq 2\pi\}$ and $y_2=\frac{1}{2}\sin(2x)\; \{0 \leq x\leq \pi\}$" />

However to compare two functions which are distinct, multiplying $x$ and $y$ by $n$ will not suffice for proving similarity. The formula to find the dilation factor can be used to prove similarity between two functions. By describing a function geometrically it has three superficial 'edges' which can be represented as sets. Two of the edges are the two axis $x$ and $y$. The length of the side '$y$' is the $\max \{ f(x) : x = 1 .. n \}-\min \{ f(x) : x = 1 .. n \}$ and the length of the side $x$ is $b_1$-$a_1$ where $b_1$ is the upper bound and $a_1$ is the lower bound. Finally the third side of the function will be the arc length over the interval $\{a_1\leq x\leq b_1\}$. Another characteristic for two shapes to be geometrically similar is the area is increased by the dilation factor squared.Thus from the formula for the dilation factor for two similar triangles the following theorem can be derived:

Theorem Let $y_1\;\{a_1\leq x \leq b_1\}$ and $y_2\;\{a_2\leq x \leq b_2\}$ be functions whose derivative exists in every point. If both functions are geometrically similar then the following system holds: \begin{equation} \frac{1}{\big(b_1-a_1\big)}\int_{a_1}^{b_1} \sqrt{1+\bigg( \frac{dy_1}{dx} \bigg) ^{2} } dx= \frac{ 1 }{ \big(b_2-a_2\big) } \int_{a_2}^{b_2} \sqrt{1+\bigg( \frac{dy_2}{dx} \bigg) ^{2} } dx \end{equation} \begin{equation} \frac{1}{\big(b_1-a_1\big)^2} \int_{a_1}^{b_1} y_1 dx= \frac{1}{\big(b_2-a_2\big)^2}\int_{a_2}^{b_2} y_2dx \end{equation}

Similarity Between Distinct Functions

When describing a function as distinct it denotes that the functions have different bases, i.e. sinusoidal and exponential. As mentioned above, for geometric similarity to exist of a function $y=f(x)$ the resultant function will become $ny=f(nx)$. However if comparing functions of different bases, equations (1) and (2) are necessary to find the bounds of similarity. For example, the problem:

Find the bounds $b$ and $a$ where $e^x\;\{0\leq x\leq 1\}$ is similar to $x^2 $.

To see examples go to the above link. Any help would be much appreciated and apologies if this is crude mathematics.

Answer 1

This is wonderful! What an interesting set of ideas. It looks like you're saying:

1. Functions of the same form (such as quadratics) can be geometrically similar to each other— they are related to each other by a change of scale.

2. By extension, you identify three important geometric properties of these (graphs of) functions: they have proportional (a) width, (b) height, and (c) area, and the proportionality factor for area is the square of the factor for length.

3. Based on these four factors, you can define similarity between functions of different kinds (such as a quadratic and an exponential). They are similar, by definition, whenever they have proportional (a) width, (b) height, and (c) area. In fact, because the functions have different forms, it is even interesting when they are just equal (proportional with a factor of 1).

4. You suggest an interesting theorem, such as: arguing from similar (infinitesimal) triangles, if two (graphs of) functions are similar, then their average arc lengths are proportional by the same factor.

5. You deploy a suite of calculation methods to find intervals over which $x^2$ and $e^x$ are similar to each other in this sense.

6. You suggest a theorem that the derivatives of similar functions are similar over the same regions.

These are all interesting explorations of the idea, and your writing does a good job of communicating them. I have read some mathematical papers that prioritize definitions and symbols before telling the reader the most important ideas and explaining where they come from. I liked that you do a good job of explaining that your ideas of geometric similarity of function graphs come from extracting ideas from geometric similarity of functions. Also, I liked

I think you could make your paper even better by clearly separating out the definition of geometric similarity of different functions. That is, you could write, in its own paragraph, "Definition: Two functions are geometrically similar if ... "

This modification has three advantages. First, it highlights your innovative contribution (the definition) by separating it a little from the discussion of concepts that have come before, i.e. similarity of triangles, and similarity of functions of the same form. Second, it helps readers (like me) remember the difference between which properties are your definition of similarity (proportional length, width, area), and which properties are theorems that you derive from your definition (proportional arc length). Third, often readers like me want to look back up to check your definition; separating out the definition makes it easy to refer back to.

All in all, I enjoyed reading your paper, and the different directions and approaches you took in investigating the ideas.

Answer 2

I love seeing a high school student interested in exploring these kinds of questions! Your thinking is right on track: take a hard problem (finding these similarities) and try to express it in terms of some simpler, more computable conditions (the arc length and area). I expect you should be able to prove your theorem with some simple change of coordinates, aka "$u$-substitution".

However, I doubt that the two conditions you state in your theorem (about the area and arclength) will be sufficient to ensure two functions are similar. Even if you add in the information about the ratio of the "height" and "length", what you might call the aspect ratio, I really doubt you'd have enough information to tell if two functions are similar. Essentially, all of your measurements are sort of large scale, but similarity will be much more attuned to the small scale behavior of your functions.

First as a simplification, if two functions were similar then we could apply the similarity and see them defined on the same domain with the same range. So I want to find two differentiable functions which share the same domain and range, have the same integral, and have the same arclength, yet are not identical. For instance, you could just look at $\sin x$ and $\cos x$ defined on $0 \leq x \leq 2\pi$. Maybe that's not the best example since these functions are similar on a smaller domain. But it gets the point across: just measuring the total arclength and integral doesn't tell you where the length and area are actually distributed across the domain. You give yourself too much freedom to work with.