Area inside a sextic curve. $y^6 + x^4 = 36xy + 4$

Question

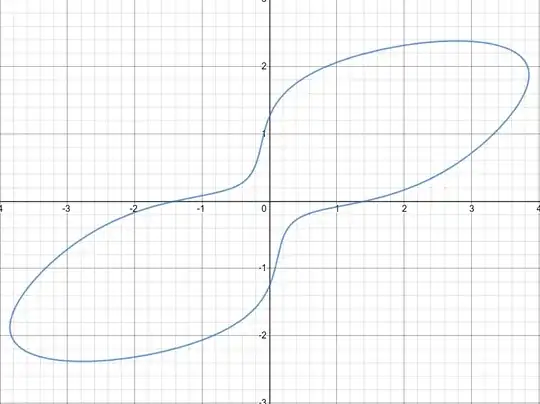
I help out high school students do their homework, and one of them said that this was a curve given to them to find the area of, using solely geometric arguments. (Pre-algebra he claims, but the formula clearly has $x$ and $y$.)

$$y^6 + x^4 = 36xy + 4$$

I actually haven't been able to find the area of this curve via any method and I've been trying for several hours over the course of a few different days. I've attempted the following:

Direct integration of the area over x.
Polar integration.
Attempting to change coordinate axes to try to remove the cross term. (I was hoping it would make a nice enough angle with the x or y axis, but it didn't).
Attempting a different form of polar integration (over $\text{d}r$ instead of $\text{d}\theta$, I figured if I could come with with a function that gave the angle subtended by curve at a particular radius it might be more amenable to integration).
Finding a parametrization of the curve and then calculating the line integral to determine the area using Green's theorem. (I don't think a natural parametrization of the curve exists? But I'm just exploring this topic for the first time as a result of this problem. The curve seems to have genus 10, and parametrization techniques requires genus 0.)

I've had little success with any approach, and I'm completely out of ideas. And while it's entirely plausible that this student is either lying to troll me and waste my time (because lol internet), or there was a misprint in the student's worksheet, this problem is still interesting enough that I cannot just let it go.

Does anyone have any good ideas on how to approach this problem?

Perhaps the instructor wants an approximation by counting boxes ... — Ethan Bolker, Oct 16 '20 at 00:01
there is an application of Green's theorem in multivariable calculus https://mathinsight.org/greens_theorem_find_area This is the principle of the https://en.wikipedia.org/wiki/Planimeter — Will Jagy, Oct 16 '20 at 00:01
@WillJagy as mentioned, I attempted to use Green's Theorem, but I could not find a parametrization of the curve. Perhaps I'm just bad at it though? — OmnipotentEntity, Oct 16 '20 at 01:10
@EthanBolker that might be true, if so it would also be rather funny. — OmnipotentEntity, Oct 16 '20 at 01:11
The substitution $y=\sqrt{s}$, $x=t\sqrt{s}$ transforms the curve into $s^3+t^4s^2=36ts+4$ (and the Jacobian determinant is a constant). This equation is cubic in $s$, so conceivably the Cardano formula might help? Seems unlikely to work... — Julian Rosen, Oct 16 '20 at 15:51
The approximate area of this region is 14.476382963592632 according to my CAS. — OmnipotentEntity, Jul 31 '23 at 14:51

Area inside a sextic curve. $y^6 + x^4 = 36xy + 4$

0 Answers0