Does the error always decrease as n increases?

Question

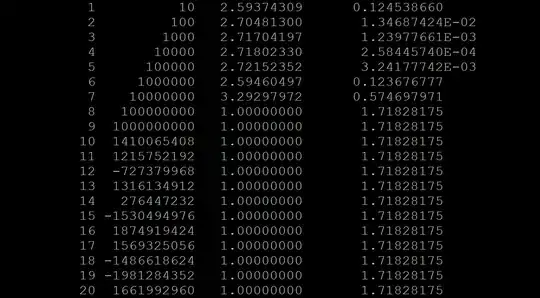
Considering the program below that calculates the mathematical constant,e from the definition, $$e = \lim_{n\to \infty}\left(1+\frac{1}{n}\right)^n. $$

It computes $\left(1+\frac{1}{n}\right)^n$ for $n=10^k$, $k=1,2,..20$.

Program: Program EApprox implicit none

integer :: n, k
real :: f, abs_error
do k = 1, 20
    n = 10(k)
    f = (1.0 + 1.0/real(n))(n)
    abs_error = abs((exp(1.0)) - ((1.0 + 1.0/real(n))*n))
    write(,*) k, n, f, &
                             abs_error
end do

End Program EApprox

Results:

Does the error always decrease as n increases?

Here are some points that I would like further clarifications on:

what you see there in terms of the behavior of the error as $n$ increases.
For the first few results, when $n$ increases by a factor of $10 $ what happens to the error? By what rate does it decrease?
And then we reach a point, where the error starts to grow. What do you think might be causing that error growth? And as $n$ continues to decrease by a factor of 10, what is the rate of increase of the error?
Here, is it possible to identify that the truncation error behaved like $O(h)$. and that the roundoff error behaved like $O(1/h)$? If yes, how so?

$(1+1/n)^n$ increases with $n$ (see for example https://math.stackexchange.com/q/515317/42969), which means that the error term decreases. The problem with your program is that computers have only a limited floating point precision: If $n$ is large then $1.0 + 1.0/n$ is rounded to $1.0$. — Martin R, Oct 15 '20 at 08:51
A reading is Is floating point math broken? on Stack Overflow, and What Every Computer Scientist Should Know About Floating-Point Arithmetic — Martin R, Oct 15 '20 at 08:55

score 0 · Answer 1 · answered Apr 24 '25 at 15:53

Yes, the error is decreasing as $n$ increases.

Let’s define the function $f: \mathbb{R} \to \mathbb{R}$ by

$$f(x) = \left(1 + \frac{1}{x} \right)^x.$$

Then we can show that $f(x)$ is an increasing function. One way we can do that is by looking at the derivative

$$f’(x) = \frac{\left(\frac{x + 1}{x}\right)^{x} \, \left(\left(x + 1\right) \ln\left(\frac{x + 1}{x}\right) - 1\right)}{x + 1} $$

which you can see is positive for $x>0$ by considering each part of this expression successively (e.g. $\frac{x+1}{x} > 0$ so $(\frac{x+1}{x})^x > 0$, etc.)

As $f(x)$ is an increasing function which tends to $e$, we have $f(x) < e$ for all $x$ and that the error

$$e - f(x)$$

is a decreasing function.

More helpful IMO is the series expansion in the exponent $(1+1/n)^n = \exp(n\ln(1+1/n))=\exp(1-1/(2n)+1/(3n^2)\pm...)$ which tells that the relative error is $-1/(2n)$ plus smaller terms. — Lutz Lehmann, Apr 24 '25 at 17:04

Does the error always decrease as n increases?

1 Answers1