Here is a strategy to find such root subsystems for irreducible (reduced) root systems:
Take the extended Dynkin diagram of the root system you're looking at, and remove one of the vertices (and the edges touching it). You are left with a Dynkin diagram of the same rank as the original one, and this gives a root subsystem.
This gives the following proper root subsystems of full rank:
- For type $A_n$: None
- For type $B_{n\ge 3}$: $D_i \times B_{n-i}$ (for $ 2\le i \le n$)
- For type $C_{n\ge 2}$: $C_i \times C_{n-i}$ (for $ 1\le i \le n-1$)
- For type $D_{n\ge 4}$: $D_i \times D_{n-i}$ (for $2 \le i \le n-2$)
- For type $E_6$: $A_1 \times A_5$ and $A_2 \times A_2 \times A_2$
- For type $E_7$: $A_1 \times D_6$, $A_2 \times A_5$, $A_3 \times A_3 \times A_1$, and $A_7$
- For type $E_8$: $A_1 \times E_7$, $A_2 \times E_6$, $A_3 \times D_5$, $A_4 \times A_4$, $A_5 \times A_1 \times A_2$, $A_7 \times A_1$, $D_8$ and $A_8$
- For type $F_4$: $A_1 \times C_3$, $A_2 \times A_2$, and $B_4$
- For type $G_2$: $A_1 \times A_1$ and $A_2$.
Added: In the first version of this answer, I thought this (with iteration, see below) would be enough, but it is not. For example, the inclusion $D_n \subset C_n$ does not show up yet. In a way, this procedure only "sees" subsystems which contain the highest root, which is always a long root. In the case of BCFG root systems i.e. those with two different root lengths, we also have to look at an extension of the Dynkin diagram with the (negative of the) highest short root, and then erase one of the other vertices. The diagrams look like this:
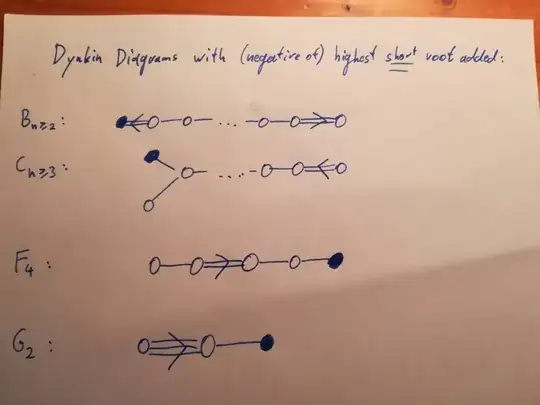and we get the following possibilities which have not already been listed:
- For type $B_{n\ge 3}$: $B_i \times B_{n-i}$ (for $ 1\le i \le n$)
- For type $C_{n\ge 2}$: $D_i \times C_{n-i}$ (for $ 2\le i \le n$)
- For type $F_4$: $C_4$, $A_1 \times A_3$, and $B_3 \times A_1$
I have a feeling, but no rigorous proof yet, that this plus the following iteration procedure exhausts all possibilities.
One word about why this procedure with the Dynkin diagram first extended by the negative of the highest, or highest short, root works: Well, what we are doing with such extended Dynkin diagrams is writing down the angle and length relations between some roots. As soon as he resulting diagram is a union of standard (non-extended) Dynkin diagrams, we know by the classification that the roots making up the vertices do generate a root system of the respective type. Now in both cases, when we first extend the Dynkin diagram with the negative -of-highest(-short) root vertex, and then remove a different vertex, what remains is a classical Dynkin diagram; meaning that the roots corresponding to the remaining vertices (all but one of them from the original basis, one the negative of the highest (short) root) will generate such a classical root system. And it is obviously of full rank and contained in our original root system.
Now in a second step, one can iterate the procedure until one arrives at all factors being of type $A$ (note that $A_1 =B_1 =C_1$, $B_2=C_2$, $D_2 = A_1 \times A_1$ and $D_3 =A_3$). E.g. within $F_4$ we further have
$$A_1 \times C_3 \supset A_1\times A_1 \times \underbrace{C_2}_{=B_2} \supset A_1 \times A_1 \times \underbrace{A_1 \times A_1}_{C_1 \times C_1}$$
as well as
$$B_4 \supset D_4 \qquad ( \supset \underbrace{A_1 \times A_1}_{D_2} \times \underbrace{A_1 \times A_1}_{D_2})$$
and also
$$C_4 \supset C_2 \times C_2.$$
Note that the only root systems of rank $n$ which do not contain an $n$-fold product of
$A_1$ (i.e., $n$ mutually orthogonal roots) are $A_{n\ge 2}$, $D_{ n \text{ odd}}$ and $E_6$, which matches well-known results about $-id$ being in the Weyl group or not.
This somewhat matches the (far, far more elaborate) tables at the end of R. W. Carter: Conjugacy Classes in the Weyl Group (Comp. Math. 25 no.1 (1972) p. 1-59), although in those tables, among the "$\Gamma$"'s for the exceptional root systems, only the subsystems from my first approach are listed. I am sure there is a reason for this in that paper.
Finally, to include the non-reduced and the reducible case from here should be easy.
