Equation of Cone vs Elliptic Paraboloid

Question

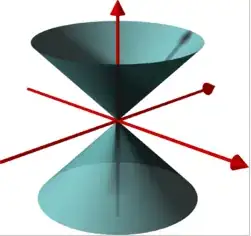
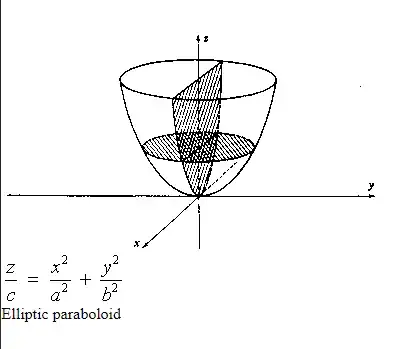
I can't understand why $$\frac{z}{c} = \frac{x^2}{a^2} + \frac{y^2}{b^2} \tag{*}$$ corresponds to an elliptic paraboloid and $$\frac{z^2}{c^2} = \frac{x^2}{a^2} + \frac{y^2}{b^2} \tag{**}$$ to a cone, and not the other way around.

I tried to understand by looking at the traces of $z(x,y)$. For example, I did so for (**):

$\boxed{\text{When } x = k:}$ Then (**) becomes: $\displaystyle \frac{z^2}{c^2} - \frac{y^2}{b^2} =\underbrace{\frac{k^2}{a^2}}_{\text{a constant}} \color{green}{\text{: hyperbolas in the $yz$-plane.}}$

${\boxed{\text{When } y = k:}}$ Then (**) becomes: $\displaystyle \frac{z^2}{c^2} - \frac{x^2}{a^2} = {\underbrace{\frac{k^2}{b^2}}_{\text{a constant}}\color{red}{\text{: hyperbolas in the $xz$-plane.}}}$

$\boxed{\text{When } z = k:}$ Then (**) becomes: $\displaystyle \underbrace{\frac{k^2}{c^2}}_{\text{a constant}} = \frac{x^2}{a^2} + \frac{y^2}{b^2} \color{blue}{\text{: ellipses in the $xy$-plane.}}$

I sketched the following shape based on this information, but it doesn't seem to tell me whether it's an elliptic paraboloid or a cone?

---

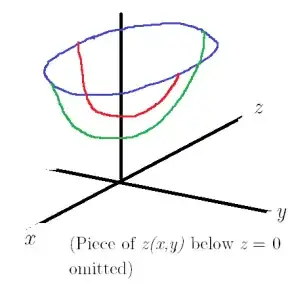
$\Large{\text{Supplementary Question:}}$ Thank you very much to all your answers, all of which helped! Based on them, the key step seems to be to look at the traces of $z(x,y)$ for $k = 0.$ I now understand that this answers my question, but why did my original work with $k \neq 0 $ fail to do so? My textbook doesn't mention the latter straightforward "trick."

---

$\Large{\text{Question S.1:}}$ @bubba: Thank you very much for your answer to the Supplementary Question. To clarify your answer, did you mean: "but, in either case, these are hyperbolas curves} unless $k=1.$" As I wrote above, for $\text{(*)}$, the traces $x=k \text{ & }y = k$ do yield hyperbolas. But for $\text{(*)}$,
$ \boxed{\text{When } x = k:}$ Then (*) becomes $\displaystyle \frac{z}{c} - \frac{y^2}{b^2} =\underbrace{\frac{k^2}{a^2}}_{\text{a constant}} \text{: PARAbolas in the $yz$-plane.}$

${\boxed{\text{When } y = k:}}$ Then (*) becomes: $\displaystyle \frac{z}{c} - \frac{x^2}{a^2} = {\underbrace{\frac{k^2}{b^2}}_{\text{a constant}}{\text{: PARAbolas in the $xz$-plane.}}}$.

Of course, the fact the traces of (*) are parabolas and NOT hyperbolas still doesn't answer my original question. As you kindly explained and I now understand, it's necessary to consider $k = 0.$

Answer 1

Something to notice is that in the equation

$$\frac{z}{c}=\frac{x^2}{a^2}+\frac{y^2}{b^2}\tag{1}$$

$z$ will either be nonnegative or nonpositive, depending on the sign of $c$. This means that this conic section will never dip below the $xy$-plane if $c$ is positive, or never rise above the $xy$-plane if $c$ is negative. Since cones look like this:

$\hspace{2.25in}$

$(1)$ must not be a cone.

Alternatively, and perhaps more enlightening, is to notice that in the equation

$$\frac{z^2}{c^2}=\frac{x^2}{a^2}+\frac{y^2}{b^2}\tag{2}$$

If we set $x=0$, that is, if we look at the intersection with the $yz$-plane, we get the two straight lines

$$y=\pm\frac{b}{c}z$$

which matches what we would expect from the picture. We get a similar result if we let $y=0$. So $(2)$ represents a cone.

Answer 2

Think about how in two dimensions, y^2 = x^2 represents a set of straight lines, while y = x^2 is a parabola.

In (*), fix x=0. Then it's easy to see that you get a parabola of the shape z = y^2 (constants ignored). Hence, the basis for an elliptic paraboloid.

In (**), fixing x=0 gives us something of the shape z^2 = y^2, or +-z = +-y. These are the straight lines needed for a cone.

Answer 3

Forget the "elliptical" part for a minute (in other words, suppose $a$ = $b$). This is just a scaling of the $x$ and $y$ axes, so it doesn't really change the problem. Then the second of your equations (**) is roughly equivalent to $\sqrt{x^2 + y^2} = mz$, where $m = 1/{c^2}$. This says the "radius" of the surface increases linearly as $z$ increases. So, it's a cone.

Answer 4

x^2/a^2 + y^2/b^2 = z/c^2 -> can not be a cone because general equation of cone is homogeneous 2nd degree equation passing through origin, since its not homogeneous so it is not cone.

for z= k^2 -> x^2/a^2 + y^2/b^2 = k^2/c^2 -> in xy plane it represent ellipse, as we increase k, size of ellipse also increase in xy plane.

in xz plane -> y=0 -> x^2/a^2 = z/c^2 -> which is a equation of parabola for z= k^2,

and in yz plane -> x=0 -> y^2/b^2 = z/c^2 -> again equation of parabola for z= k^2.

so curve thus obtained is elliptical paraboloid.

x^2/a^2 + y^2/b^2 = z^2/c^2 -> homogeneous equation of 2nd degree passing through origin, so by definition of cone , the equation represent a cone. let us visualize further:

for z=k -> x^2/a^2 + y^2/b^2 = k^2/c^2 -> represent ellipse in xy plane even power of x,y,z so symmetrical about each coordinate planes. in xz plane -> y=0 -> x^2/a^2 = z^2/c^2 -> x/a = z/c and x/a = -z/c -> pair of lines which are the generator of cone.