2

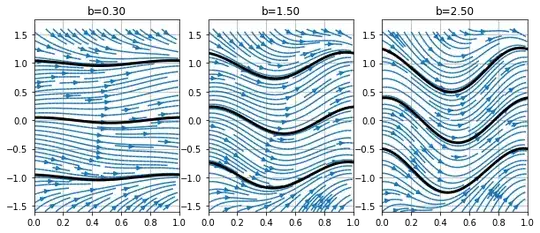
Consider a differential equation given by $x'=f(x,t)$ Depending on the parameter $ t $, that is, not autonomous. I want to understand the behavior of the solutions to these equations. For example: Consider a family of ODE's of the type: $$ x' = x - x^{3} - b\sin\left(\,{2\pi t}\,\right) $$

In order to understand the phase diagram I considered the case where $ b $ is null, thus $ b\sin (2 \pi t) $ translates $ x-x ^ 3 $ on the vertical axis. If I take $ x '= 0 $, we have $ x-x ^ 3-b\sin (2 \pi t) = 0 $ and I can find the equilibrium points. I would like to know what happens when I take small $ | b | $, or when I increase that module.

One way to study the solutions is to plot this ODE graph and analyze the bifurcation points.

Can anyone help me know if this ODE family has a periodic solution when $ | b | $ is small or large? Can I draw the line $ y = x $ and find the points of intersection with the graph $ x-x ^ 3-b\sin (2 \pi t)$ ?

Could someone show me details of whether this family has periodic solutions?

K.defaoite
  • 13,890
Gregory math
  • 101
  • 6
  • When $b$ is null, you get the equation $x' = x-x^3$. Can you solve this equation using a substitution? – Sarvesh Ravichandran Iyer Sep 23 '20 at 05:38
  • For the case where $ b $ is null, $ x = 0.1, -1 $ are breakeven points. Where $ 0 $ is source and $ -1.1 $ are skins. I would like to understand what happens when we add the term depending on $ t $. – Gregory math Sep 23 '20 at 10:05

1 Answers1

1

The function $f(x)=x-x^3$ is surjective on the real line. Thus it is always possible to find $x_b>1$ with $f(x_b)=-2|b|$, $f(x)<-2|b|$ for $x>x_b$. By symmetry $f(-x_b)=2|b|$ etc.

This gives the interval $[-x_b,x_b]$ as a trapping region, as $x'\le -|b|$ for $x\ge x_b$ and $x'\ge|b|$ for $x\le-x_b$.

If $\phi(t;t_0,x_0)$ is the flow of the ODE, then the map $x\mapsto\phi(1;0,x)$ has the image of $[-x_b,x_b]$ inside itself, which implies that a fixed point $x_*$ exists. It is now easy to prove that $\phi(t;0,x_*)$ is a periodic solution.

If $|b|<\frac1{3\sqrt3}$ is small enough, then other lines with $|f(x)|=2|b|$ can be identified around the roots $0,\pm1$ of $f$. This gives rise to periodic solutions oscillating around these roots.

Numerical experimentation suggests that the pattern of 3 periodic solutions is not only true for small $b$.

enter image description here

See Is this periodic solution unique? (ODE) (and links) for a similar problem.

Lutz Lehmann
  • 131,652
  • what about $ sin (2 \pi t)$? Because the equation depends on the parameter $ t $. Doesn't it change anything? – Gregory math Sep 23 '20 at 10:02
  • That's why the bound is chosen to be $2|b|$. So if $x>x_b$ you get $$x'<-2|b|+b\sin(2\pi t)\le -|b|$$ etc. For very large $|x|$ the right side is always dominated by $-x^3$, moving the solution towards $0$. This implies that at the boundary of falling and rising solutions there have to be periodic solutions. – Lutz Lehmann Sep 23 '20 at 10:10
  • I didn't understand how it is possible to get $ f (x_b) = - 2 | b | $. – Gregory math Sep 23 '20 at 10:16
  • Wee know that $f(1)=0$ and then it is monotonically falling towards $-\infty$. The intermediate-value theorem then tells us that there is a unique point $x_b$ where the value $-2|b|$ is taken. – Lutz Lehmann Sep 23 '20 at 10:38
  • I would like to find the Poincaré application of this ode. The first derivative in relation to $ x $ is given by

    $$1-3x^2$$ And the second derivative is given by

    $$-6x^2$$

    I would like to study the sign of the Poincaré application to find the points that this application crosses the line $ y = x $. It seems to me that it is a similar case when $ b $ is null and we have three periodic solutions $0, \pm 1$.

    I would like to plot a three-dimensional diagram with $ t, b $ varying. A phase portrait in dimension 3.

     – Gregory math Sep 24 '20 at 04:21
  • Could anyone help? – Gregory math Sep 24 '20 at 04:22
  • @Gregorymath Do you want to do this analytically or graphically? – Evgeny Sep 24 '20 at 15:57
  • Any of the options, I wanted to better understand this, qualitatively – Gregory math Sep 24 '20 at 20:33
  • @Gregorymath If you know Python/MATLAB/Mathematica/Julia (or any other high-level programming language), you can compute Poincaré map numerically. Just pick a quite dense grid of points with $x$ coordinates (for example $N = 1000$ points in segment $\lbrack -1, , 1 \rbrack$) and compute the numerical trajectory for $0 \leq t \leq 1$. Let $\tilde{x}$ be the point at which trajectory lands at $t = 1$. The mapping $\mathcal{F}\colon x \rightarrow \tilde{x}$ gives you a Poincaré map for this problem. In case of systems with periodic forcing it is also called stroboscopic map. – Evgeny Sep 24 '20 at 21:43