3

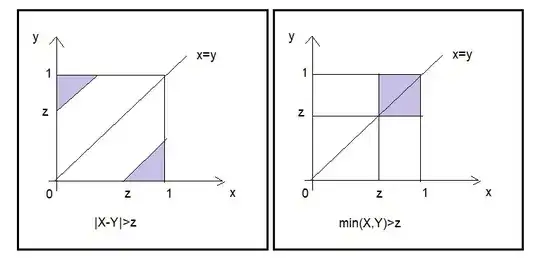
Say $X,Y \sim U(0,1)$ be two independent uniform random variables, and $T=|X-Y|$. I would like to find the CDF of $M=\max(X,Y)$, $L=\min(X,Y)$, and $T$. I find the CDF of $M$ and $L$ as $$P(M\leq t ) = P(X\leq t)P(Y \leq t) =t^2$$ $$P(L \leq t) = 1-P(X\geq t ) P(Y\geq t) = 1-(1-t)^2$$ To find the CDF of $T$, I draw a rectangle with unit length and width, and compute the area within the region $|X-Y| \leq t$, which turns out to be $1-(1-t)^2$.

My question is how come the CDF of $L$ and $T$ are the same when one is the minimum of two uniform r.vs and the other is the absolute difference of two uniform r.vs? Is there something wrong with my computation? Thanks.

StubbornAtom
  • 17,932
ForumWhiner
  • 659

2 Answers2

4

Your calculations are correct! Just for the sake of completeness, you have to write

$$F_M(t)=t^2\mathbb{1}_{(0;1)}(t)+\mathbb{1}_{[1;\infty)}(t)$$

...and similar notation for the other CDF's. This because the CDF is defined over all $\mathbb{R}$

Why the law of L and T are the same? As you did to find $F_T$ do the same drawing to find $F_L$ and you will realize that the integration area is the same

enter image description here

tommik
  • 33,201
  • 4
  • 17
  • 35
3

Imagine a line segment $OA$ of unit length.

On this line segment imagine two points $X,Y$ each at a distance of $x, y$ from point $O$ respectively.

These two points divide $OA$ into three smaller segments, whose length is equal to $min(x,y)$; $|x-y|$ and $1 - max (x,y)$.

From symmetry it can be seen that the three values should have same Expectation values.

xax
  • 295