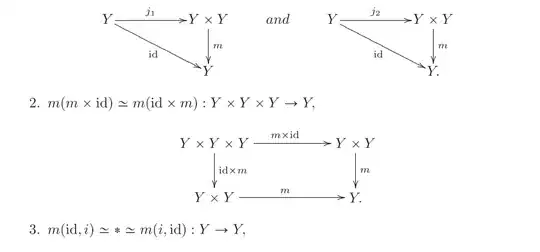
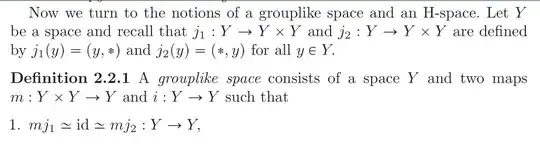Here is my definition for a grouplike space or an $H-$group from "Introduction to homotopy theory" by Martin Arkowitz:
And here is a question I found here:
Every loop space $(\Omega Y,w_0)$ has the structure of an $H$-group. that is answering my question which is Why are loop spaces $\Omega Y$ examples of grouplike spaces ?, but unfortunately I do not understand the proof in that question, so I need a proof in terms of my definition. Could anyone show me that proof, please?
Also, if anyone could explain to me how is my definition is the same as the definition given in the link above (if that is corect) I would really appreciate that.