2

Unfortunately, I am not so good in Maths and I am trying to find out a formula to calculate the sum of a spinner with $2,3$ or $4$ spins.

The spinner
The spinner has $6$ numbers (like a $6$ face dice).
Each number is different.
Each spinner sector has a different size (different probability).
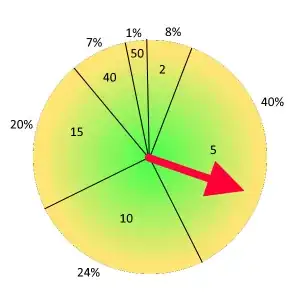
Spinner

The problem
Giving a spinner with $6$ different numbers and different probabilities for each number, how much is the probability to reach at least a number if I spin it $2$ times? Or $4$ times?

In this case, I should calculate the possibility to have a sum of $40$ or more. I am able to simulate it, but it would be nice if anyone can help me devise a formula.

gemspark
  • 340
Adriano
  • 123
  • 2
    Why do you think such a formula exists? I don't see a clear pattern in the probabilities and values, so I'm not sure you can avoid the lengthy work of going over all the possibilities one-by-one. – YJT Sep 17 '20 at 09:33
  • Related: https://math.stackexchange.com/questions/1646101/distribution-of-the-sum-of-n-loaded-dice-rolls – Matti P. Sep 17 '20 at 09:44
  • @YJT: I don't know if such a formula exists... I was thinking it could exists, because the problem seems to be easy. But the answer: "I have to go one-by-one" is also a good answer. It helps me to know that there is no way to find it through an "universal" formula. – Adriano Sep 17 '20 at 09:55

1 Answers1

1

Lets say you have the probability P of being in a state S defined as,

$P(S_2)=0.08$, $P(S_5)=0.40$, $P(S_{10})=0.24$, $P(S_{15})=0.20$, $P(S_{40})=0.07$, $P(S_{50})=0.01$,

Now if you get $50$ or $40$ in the first go, you don't need to spin the wheel anymore.

If you get any other no. you will have to spin again. Now suppose if you get $10$ and in the next spin $40$ you have already reached the sum. But if you get 15 you will again have to spin it and go through the same process.

Forming this mathematically,

Let $M_{1,40}$ be the event of reaching a sum of $40$ in $1st$ spin, then $M_{1,40} = P(S_{40}) + P(S_{50})$.

Similarly, $M_{2,40} = M_{1,40} + [P(S_{2})+P(S_{5})+P(S_{10})+P(S_{15})].[P(S_{40}) + P(S_{50})] $.

And all other calculations would go on like this.

If you want you can come up with a formula for values $A,B,C,D,E$ having probabilities $a,b,c,d,e$ by hand in a similar fashion and use it directly in simulation.

It is evident here that the minimum no. of spins required to always attain a sum of $N$ is $ceil(\frac{N}{min(A,B,C,D,E)})$.

gemspark
  • 340
  • Thank you! It helps me on the 2 spins. As the result is (0.01 + 0.07) + (1.00 - 0.01 - 0.07)*(0.01 + 0.07) = 15.36%. But as said by YJT, I have to solve it one-by-one with 3 spins and 4 spins... – Adriano Sep 17 '20 at 09:59
  • Yeah, you'll have to do that. – gemspark Sep 17 '20 at 10:01