2

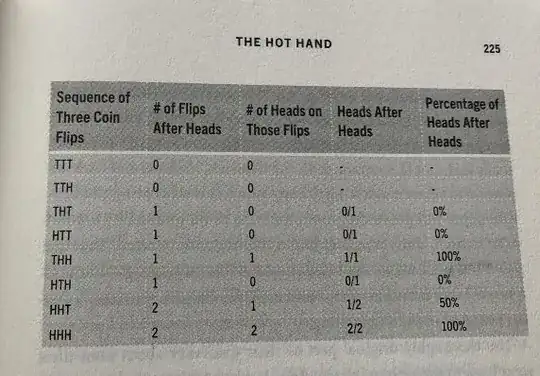
I came upon an interesting table in the book "The Hot Hand: The Mystery and Science of Streaks" by Ben Cohen:

enter image description here

In this calculation, we are considering 3-flip sequences and are measuring the percentage of the time a head occurs directly after another head, and show that it is 42% and not 50% like we may expect. Mathematically, I initially thought the calculation was the following:

$$ \begin{aligned} P(\textrm{next flip H} \mid \textrm{3-flip sequence is not TTT or TTH, previous flip is H}) = &\frac{1}{6}\frac{2}{2} \textrm{(for HHH)} + \frac{1}{6}\frac{1}{2} \textrm{(for HHT)} + \\&\frac{1}{6}\frac{0}{1} \textrm{(for HTH)} + \frac{1}{6}\frac{1}{1} \textrm{(for THH)} +\\&\frac{1}{6}\frac{0}{1} \textrm{(for HTT)} + \frac{1}{6}\frac{0}{1} \textrm{(for THT)}\\=&\frac{5}{12} = 41.667\% \end{aligned} $$

However, after thinking about this further, I am clearly not keeping track of the events properly. If we define $A = \textrm{next flip H}$, $B = \textrm{3-flip sequence is not TTT or TTH}$, $C = \textrm{previous flip is H}$, and we know that $$P(\textrm{next flip H} \mid \textrm{3-flip sequence is not TTT or TTH, previous flip is H}) = P(A \mid B, C)$$

We get:

$$ \begin{aligned} P(A, C \mid B) = &\frac{1}{6}\frac{2}{2} \textrm{(for HHH)} + \frac{1}{6}\frac{1}{2} \textrm{(for HHT)} + \frac{1}{6}\frac{0}{2} \textrm{(for HTH)} + \frac{1}{6}\frac{1}{2} \textrm{(for THH)} +\\&\frac{1}{6}\frac{0}{2} \textrm{(for HTT)} + \frac{1}{6}\frac{0}{2} \textrm{(for THT)} = \frac{1}{3}\\ P(C \mid B) = &\frac{1}{6}\frac{2}{2} \textrm{(for HHH)} + \frac{1}{6}\frac{2}{2} \textrm{(for HHT)} + \frac{1}{6}\frac{1}{2} \textrm{(for HTH)} + \frac{1}{6}\frac{1}{2} \textrm{(for THH)} +\\&\frac{1}{6}\frac{1}{2} \textrm{(for HTT)} + \frac{1}{6}\frac{1}{2} \textrm{(for THT)} = \frac{2}{3}\\ P(A \mid B, C) = \frac{P(A, C \mid B)}{P(C \mid B)} = &\frac{\frac{1}{3}}{\frac{2}{3}} = \frac{1}{2} \neq \frac{5}{12} \end{aligned} $$

My question is what does the $41.667\%$ represent in conditional probabilities, and what does it actually communicate to us about the hot hand? Intuitively, I understand why the probability expressed is not $50\%$ (there is already a great post explaining this much), but I have not been able to articulate the probability it is representing.

EDIT: There seems to be confusion on what I am hoping to learn here. I am not trying to find $P(\textrm{next flip H} \mid \textrm{3-flip sequence is not TTT or TTH, previous flip is H})$ or $P(A, C \mid B)$ in probability. I am trying to understand what the $41.667\%$ is actually representing. The author's argument hinges on this calculation (which I expressed on the right hand side of the first block of calculations) not being equal to $50\%$, and I am confused what the $41.667\%$ actually represents.

Morris Greenberg
  • 73
  • Which subset of ${TTT,TTH,THT,HTT,THH,HTH,HHT,HHH}$ (i.e., which event) corresponds to the statement "next flip $H$"? – John Dawkins Sep 13 '20 at 18:23
  • We have eight possible outcomes, ${HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}$, all of the same probability. Three of them have head followed by head, i.e. contain $HH$. Shouldn’t the answer thus be 3/8=37.5%? – sampleuser Sep 30 '20 at 16:01
  • It is not clear what probabilities you calculate. A standard way to calculate such probabilities it to provide a finite set $\Omega$ of elementary events and for each $\omega\in\Omega$ its a value $p_\omega$. Then events are subsets of $\Omega$ and a probability $P(A)$ of an event $A\subset\Omega$ equals $\sum_{\omega\in A} P(A)$. For instance, when we consecutively toss three coins we have a space $\Omega$ consisting of eight sequences of head and tails of length $3$. Put $p_\omega=1/8$ for each such sequence $\omega$. – Alex Ravsky Sep 30 '20 at 19:09
  • Then an event $B$ "3-flip sequence is not $TTT$ or $TTH$" has probability $P(B)=6/8$. But is is not clear which subset of $\Omega$ correspond to an event “next flip is $H$” or to an event “previous flip is $H$”. – Alex Ravsky Sep 30 '20 at 19:09
  • 1
    Thanks, Alex. To be clear, I am trying to define what the calculation represents that the author did on the right hand side. I agree that your approach makes more sense to me in calculating probabilities, I am just trying to understand what 42% represents when he says 42% is not 50%. – Morris Greenberg Sep 30 '20 at 23:36
  • While I'm still chewing on this myself, I'm pretty sure a substantial rationale for it is the finite number of flips; that is to say, if you were to flip an arbitrary number of times, this probability would go to $\frac12$ as you would expect. – Steven Stadnicki Sep 30 '20 at 23:55

2 Answers2

1

$\require{cancel}$ If you're analyzing some data trying to empirically determine whether "streaks" really exist or not, 5/12 is the probability of getting a post-streak success in the "boring world" where successes behave like independent coin tosses. If you weren't being careful, you might assume the boring-world probability of a post-streak success is exactly 50%. It's actually less, because of the way after-the-fact filtering for streaks biases the choice of what comes after the streak.

Establishing the correct baseline number 5/12 is important when you return to examining your data. After all, if you compute the same statistics on your data and you get a number larger than 5/12 --- say 50% --- you should correctly interpret this as fairly significant evidence against the boring world hypothesis and evidence in favor of the hot-hand hypothesis.

If you would like to represent 5/12 as a conditional probability, let:

  • $A$ = You pick a sequence of three coin flips.
  • $B$ = You pick a pair in the sequence.
    • $H_1$ = the first element is heads. $H_2$= the second element is heads.
  • $\widehat B$ = You pick a (possibly different) pair in the sequence.
    • $\widehat H_1$ = the first element is heads. $\widehat H_2$= the second element is heads.

The observation is that, in the boring world, $$\Pr(\widehat H_1 \widehat H_2 | A,\,BH_1,\,\widehat{B}) = \frac{5}{12}$$

This is because of the filtering effect of having $BH_1$ as given— filtering for triples with potential 2-streaks in them.

We can calculate this conditional probability using Bayes' law (Note: Instead of writing $BH_1$ and $\widehat{B}\widehat{H}_1$, I'll leave the $B$ implied and just write $h_1$ and $\widehat{h}_1$ so as to make it easier to read. You could also suppress $A$, which appears as given in all terms.):

$$\Pr(h_1 | A) \cdot \Pr(\widehat{h}_2\widehat{h}_1 | h_1\, A) = \Pr(\widehat{h}_2\widehat{h}_1 | A) \cdot \Pr(h_1\,| \widehat{h}_2\widehat{h}_1\, A) $$

We can straightforwardly compute three of these conditional probabilities, solving for the one we want $\Pr(\widehat{h}_2\widehat{h}_1 | h_1\, A)$.

Now,

  • $\Pr(h_1 | A) = \frac{1}{2}$. If you pick a random pair from a random triple, then 8 out of the 16 possible pairs have heads first.
  • $\Pr(\widehat{h}_2\widehat{h}_1| A) = \frac{1}{4}$, because among all triples, 4 out of 16 pairs are HH.
  • $\Pr(h_1 | \widehat{h}_2\widehat{h}_1\, A) = \frac{5}{6} $, because if you filter for triples with HH (THH, HHT, HHH), then 5 out of 6 possible pairs start with H.

So

$$\frac{1}{2}\cdot \Pr(\widehat{h}_2\widehat{h}_1 |\, h_1 A) = \frac{1}{4}\cdot \frac{5}{6}$$

$$\Pr(\widehat{h}_2\widehat{h}_1 |\, h_1 A) = \frac{5}{12}$$

which we wanted to establish.

user326210
  • 19,274
0

Suppose there are eight doors with the letters TTT, TTH, THT, HTT, THH, HTH, HHT, HHH respectively on a sign over each door. The first two doors are locked with obvious padlocks, so we choose one of the other six at random. Inside the room are three large letters on the wall, the same as the sign over the door. We stand in front of an H that is not the third letter (if there are two such H's, we choose one at random). Then we look at the letter to the right. What is the probability it is H?

The answer to that question is $41\frac23 \%.$

What does this have to do with sequences of coin tosses? Not much.

If you walked into a room during a sequence of three coin tosses while the coin was still spinning during one toss, and all you knew was that the third toss had not yet occurred and the toss that had just occurred was heads (because you were present when it came to rest heads up), the conditional probability that you are have just walked in on one of the two HHx sequences (given what you know) is twice as high as the conditional probability that you are have just walked in on one of the two HTx sequences (given what you know). The same is true if we compare HHx to THx. If you give the same weight to HTx as to HHx in the calculation of the "probability" of a head, you simulate a situation like the eight doors, not like actual sequences of coin tosses.

Here's another table: $$ \begin{array}{lllll} {\text{sequence}\\\text{of three}\\\text{coin flips}} & {\text{# of flips}\\\text{after heads}\\\text{or tails}} & {\text{# of "same}\\\text{as previous"}\\\text{on those flips}} & {\text{same as}\\\text{previous}} & {\text{percentage}\\\text{of same as}\\\text{previous}} \\ TTT & 2 & 2 & 2/2 & 100\% \\ TTH & 2 & 1 & 1/2 & 50\% \\ THT & 2 & 0 & 0/2 & 0\% \\ THH & 2 & 1 & 1/2 & 50\% \\ HTT & 2 & 1 & 1/2 & 50\% \\ HTH & 2 & 0 & 0/2 & 0\% \\ HHT & 2 & 1 & 1/2 & 50\% \\ HHH & 2 & 2 & 2/2 & 100\% \\ \end{array} $$

Now take the average percentage of "same as previous flip" and you will get $\frac12$ or $50\%$. The difference here is that we are counting equally likely conditions equally.

David K
  • 108,155
  • 1
    Thanks for the response, David. The part here that is missing to my question was what does it represent in terms of conditional probabilities. What events are we explicitly conditioning on to generate this 5/12 calculation? For motivation, the author's argument is that the hot hand partially exists because for events we think intuitively as occurring 1/2 of the time, they actually occur 5/12 of the time. What events are we conditioning on to produce this outcome? What is our intuition explicitly missing? – Morris Greenberg Oct 06 '20 at 16:55
  • Our intuition is missing nothing. The $5/12$ is a nonsensical result that the author got by improperly accounting for the conditional probabilities. When we correctly account for the conditional probabilities, as I did above, we get a $1/2$ result that happens also to agree with intuition. There is no good explanation for the author's result in terms of conditional probability of events in a sequence of coin tosses. This is because the author's argument is simply incorrect. – David K Oct 07 '20 at 03:15
  • By the way, I have no doubt that there can be a "hot hand" in various types of endeavor. Certainly in a game of skill it is believable. (The skill could be the skill to toss a coin so it comes up heads more than 50% of the time, in which case all the tables in on this page, including Cohen's, are irrelevant.) But the idea of a "hot hand" in the toss of a fair coin is a variation of the gambler's fallacy. – David K Oct 07 '20 at 03:36