0

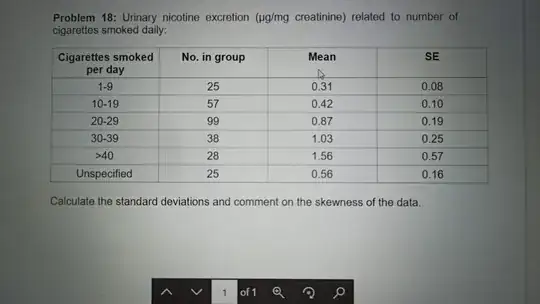
So in class we were asked to find the mean and SD for the given dataset belowenter image description here

The data set represents a sampling mean distribution for cigarettes smoked per day and no of people in each group. I could easily calculate mean using the formula as $\frac{\sum f_ix_i}{\sum f_i}$. However the question asks to find Standard deviations so does that mean for every row I need to calculate a different SD using $$\text{SE}=\frac{\sigma}{\sqrt{n}}$$. But that would be wrong as all the data sets are picked from the same population so they cant give different SDs. Also to find skewness I need to find SD of the population. Will it be just the SD of means or will it be something different?

Archis Welankar
  • 16,138

2 Answers2

1

Remember, you're not finding $\sigma$. That's the standard deviation of the entire population. You're finding $s$, the standing deviation of the sample.

The formula you provided to calculate $\bar{x}$, namely $\bar{x}=\frac{\sum f_ix_i}{\sum f_i}$, is what you would use to approximate the mean of grouped data. You typically would choose $x_i$ to be the class midpoint when applying this formula to approximate $\bar{x}$.

You can actually calculate the exact value of $\bar{x}$ by multiplying the mean of a given class with its corresponding No. in group, adding up those values, and then dividing by $\sum f_i$.

You can calculate $s$ by squaring SE, multiplying by (No. in group)(No. in group $-$1), adding up those values, dividing by $\sum f_i-1$, then taking a square root.

You can approximate both of these statistics by using the first two columns of the table. But who would approximate if you can get the exact values?

Lastly, can you quickly assess the shape of the dataset by inspecting the frequencies of the classes? If you constructed a histogram for this dataset, what would its shape be?

  • I cant inspect the shape as the last row mentions unspecified so my shape would depend on where I put those people. If I am mistaken please correct me. Also can you tell me the link from where you got that formula for SD. – Archis Welankar Sep 09 '20 at 06:48
  • Also i am confused about the data this data has different groups so does that mean that each group has been sampled from a different population. – Archis Welankar Sep 09 '20 at 06:51
1

Judging from the way the question is phrased in the screen capture, I presume that the calculation for the overall sample variance should be simply $$s^2 = \frac{1}{N - 1} \sum_{i=1}^m (n_i - 1) s_i^2, \tag{1}$$ where $N$ is the overall sample size, $n_i$ is the sample size of group $i$, and $s_i^2$ is the sample variance of group $i$, in this case $$s_i^2 = n_i SE_i^2,$$ where $SE_i$ is the standard error of group $i$.

However, the basis for this calculation assumes that the within-group sample means are equal. If they are not, then this calculation is only an approximation, because the overall sample variance is based on the squared deviations from the overall mean, not the within-group means. I discussed this issue in two other posts here:

Can I work out the variance in batches?

How do I combine standard deviations of two groups?

However, the calculation for six groups is going to be somewhat tedious and not recommended without a computer. It is a common misconception (hence, the existence of questions like these) that the overall sample standard deviation has no contribution from the variation that exists between groups.

Allow me to illustrate with the computation with only the first two groups. The table may be written as $$\begin{array}{c|ccc|cc} i & n_i & \bar x_i & SE_i & s_i^2 & (n_i - 1)s_i^2 \\ \hline 1 & 25 & 0.31 & 0.08 & 0.16 & 3.84 \\ 2 & 57 & 0.42 & 0.10 & 0.57 & 31.92 \\ \end{array}$$

Then we can agree that the overall sample mean for the first two groups is $$\bar x = \frac{n_1 \bar x_1 + n_2 \bar x_2}{n_1 + n_2} = 0.386463.$$ The supposed overall sample variance would be, according to formula $(1)$ above, $$s^2 = \frac{1}{25+57 - 1} \left( (n_1 - 1)s_1^2 + (n_2 - 1)s_2^2 \right) = \frac{3.84 + 31.92}{81} = 0.441481.$$ But as I stated above, this is incorrect. The correct formula contains the additional term $$\frac{n_1 n_2 (\bar x_1 - \bar x_2)^2}{(n_1 + n_2)(n_1 + n_2 - 1)} = \frac{25(57)(.31 - .42)^2}{(25+57)(25+57-1)} = 0.00259598,$$ making the true overall sample variance equal to $$s^2 = 0.441481 + 0.00259598 = 0.444077$$ for the first two groups. If so inclined, you could repeat this calculation on the next two groups, and then the last two groups, giving you three pairs of aggregated sample means and sample variances. Then you could merge these two at a time with two more calculations. But this is not what I think the author of the question had in mind when it was written, because the exact formula I am using, with the adjustment for between-group variance, is not commonly known even to experienced statisticians.

heropup
  • 143,828
  • Thanks for the nice explanation here and in other two posts. 1 question which I had is that the last row mentions unspecified so wont that affect the data distribution(and eventually the mean)as I can put those people anywhere I want in the data set without restriction. – Archis Welankar Sep 09 '20 at 07:26
  • @ArchisWelankar No. We don't care about what each group represents. The cigarette smoking frequency data is itself irrelevant if all we want to do is compute the overall sample mean and variance, because each measurement was observed for a unique experimental unit--i.e., no person in this table was represented more than once. – heropup Sep 09 '20 at 07:32
  • @ArchisWelankar Another way to think about it is that smoking frequency is a covariate. You could have been presented with a table that instead categorized individuals based on their sex, or their age group, or their race/ethnicity. The number of groups and their data would look different, but the nicotine excretion statistics for the aggregate/overall cohort would be the same no matter how they are categorized, so long as every measurement is included exactly once. – heropup Sep 09 '20 at 07:36
  • @ArchisWelankar That said, if you are to comment on the relationship between smoking frequency and nicotine excretion rate, then the last category, "Unspecified," is problematic because as you pointed out, it is not numeric. A reasonable approach would be to ignore this group when computing the overall mean and variance for the purpose of commenting on skewness. – heropup Sep 09 '20 at 07:39
  • It's really nice that you took so much effort to put it out clearly. I have been scratching my head for this problem to make sense and it does make now. Also skewness of the whole data can be found out plotting the means vs frequency(no.of people),right, or is there any analytical predictive modelling to find skewness of the samples. – Archis Welankar Sep 09 '20 at 07:41