A Conic Can Be Drawn through Any Five Points

Question

Hy,

I'm studying the old article A Conic Can Be Drawn through Any Five Points (E. Budden,The Mathematical Gazette, pp. 145-151, 1898) (JSTOR link). I want to get this result using only Euclidian and analytic geometry as he had done.

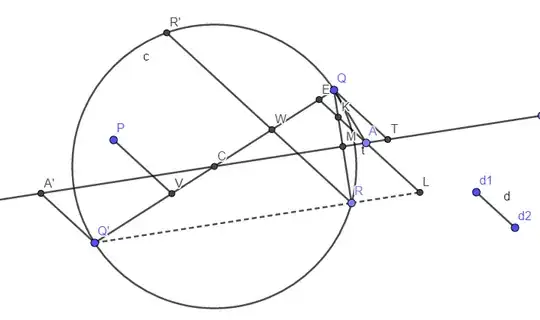
I understand all the construction done in the article and get the following figure. $A'Q', QT, PV, R'R, EA, d_1d_2$ are all parallels. $Q'L$ and $CT$ are parallels. $QR$ and $CT$ are perpendicular.

My doubt is when he writes "Construct the conic with major axis $AA'$, and semi-minor axis $CB$ given by the relation" $$\frac{(BC)^2}{(AC)^2}=-\frac{(QM)^2}{MA.MA'}$$

I really don't know how to do it and if the minus signal is a typo or a notation.

Thanks a lot if you could help me or indicate me some similar work. I searched at the forum and I just found another ways to prove the result, none of them using only basic Geometry..

Thanks a lot

It would be helpful to add a photo of the page with that construction. — Intelligenti pauca, Sep 05 '20 at 15:04
For a geometric construction of the ellipse through five points (but the construction for a hyperbola is analogous) see here: https://math.stackexchange.com/questions/3744992/find-the-properties-of-an-ellipse-from-5-points-in-3d-space/3745328#3745328 — Intelligenti pauca, Sep 05 '20 at 15:49
@JeanMarie: You can view the article on JSTOR. JSTOR usually restricts free access to a handful of articles per month; out of consideration for the COVID-19 pandemic, that limit has been raised to 100/month. — Blue, Sep 05 '20 at 19:02
Thanks for the comments and for add the JSTOR link in the question. I didn't put the picture of the page because I don't know if the forum allow us to do it. — Cleto Pereira, Sep 05 '20 at 21:43

Intelligenti pauca · Answer 1 · 2020-09-05T20:29:44.170

1

Even if not explicitly stated, the author is using signed segments: a segment on a line can be positive or negative according to an arbitrarily chosen direction on the line. In particular, it is always true that $AB=-BA$.

In your case, segments $MA$ and $MA'$ have opposite signs and their product is therefore negative: that explains why a minus sign on the right hand side is needed.

edited Sep 05 '20 at 20:29

answered Sep 05 '20 at 18:42

Intelligenti pauca

55,765

A Conic Can Be Drawn through Any Five Points

1 Answers1