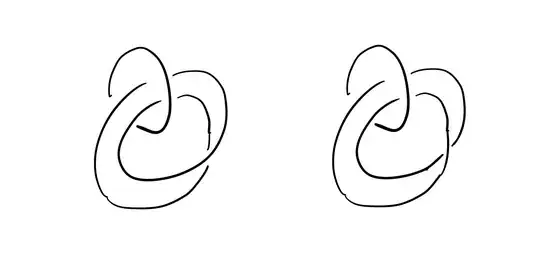
Are the following two links equivalent (orientation preserving isotopies)?
The two links have the same linking number. The only difference is the crossing that in one case is positive while in the other negative. In other words, the writhe of the curled component is different (but the writhe is not invariant under the first Reidemeister move).
The most naive approach would be to rotate part of the picture but these kind of transformations cannot change the writhe.
Motivation: This kind of pictures pop up in studying Kirby diagrams of $\mathbb{D}^2$ bundles over $\mathbb{RP}^2$. In particular I expect them to be equivalent.