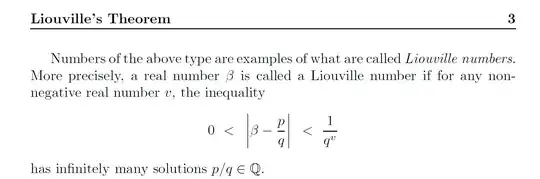Prove that the reciprocal of a Liouville number is also a Liouville number
I am using the definition of a Liouville number given in the book Transcendental Numbers by M. Ram Murty. A screenshot of the definition is attached
Proof: Let, if possible, $\frac{1}{\beta}$ is not a Liouville number where $\beta$ is a Liouville number. Then, $\exists$ a non-negative real number $v_0$ such that for any non-zero rational number $\frac{p}{q}$ such that $\gcd(p,q)=1$ and $q\neq0$, we have, \begin{gather*} \left|\frac{1}{\beta}-\frac{p}{q}\right|\geq\frac{1}{|q|^{v_0}}\tag{1} \end{gather*} Since $\beta$ is a \textit{Liouville number}, for any $v\in\mathbb{R}_{\geq0}$, there exists a rational $\frac{p_v}{q_v}$ such that $\gcd(p_v,q_v)=1$, $q_v>0$ and, \begin{gather*} 0<\left|\beta-\frac{p_v}{q_v}\right|<\frac{1}{q_v^v}\tag{2} \end{gather*} For any positive integer $m$, there are only finite number of rationals in reduced form with denominator $m$ which satisfy the Liouville's condition. Therefore, it's clear that $q_v\rightarrow\infty$ as $v\rightarrow\infty$. Also, since $|\beta|$ is a finite positive quantity, all but at most a finite number of $\frac{p_v}{q_v}=0$. Therefore we can extract a strictly increasing sequence of non-negative reals $\{v_n\}_{n\geq1}$ such that $\frac{p_{v_n}}{q_{v_n}}\neq0$. Therefore, combining $(1)$ and $(2)$ we get, for any $n\geq1$ the follwing facts, \begin{gather*} 0<\left|\beta-\frac{p_{v_n}}{q_{v_n}}\right|<\frac{1}{q_{v_n}^{v_n}}\\ \implies \left|\frac{q_{v_n}}{\beta p_{v_n}}\right|\frac{1}{q_{v_n}^{v_n}}>\left|\frac{1}{\beta}-\frac{q_{v_n}}{p_{v_n}}\right|\geq\frac{1}{\left|p_{v_n}\right|^{v_0}}\\ \implies\left|\frac{q_{v_n}}{\beta p_{v_n}}\right|\frac{\left|q_{v_n}\right|^{v_0}}{q_{v_n}^{v_n}}\geq1\tag{3} \end{gather*} Since \begin{gather*} 0<\left|\beta-\frac{p_{v_n}}{q_{v_n}}\right|<\frac{1}{q_{v_n}^{v_n}} \end{gather*} and \begin{gather*} \lim_{n\rightarrow\infty}\frac{1}{q_{v_n}^{v_n}}=0 \end{gather*} we have, \begin{gather*} \lim_{n\rightarrow\infty}\left|\frac{p_{v_n}}{q_{v_n}}\right|=|\beta| \end{gather*} Therefore we have, \begin{gather*} \lim_{n\rightarrow\infty}\left|\frac{q_{v_n}}{\beta p_{v_n}}\right|\frac{\left|q_{v_n}\right|^{v_0}}{q_{v_n}^{v_n}}=\lim_{n\rightarrow\infty}\left|\frac{q_{v_n}}{\beta p_{v_n}}\right|\left|\frac{q_{v_n}^{v_0}}{q_{v_n}^{v_0}}\right|\frac{1}{q_{v_n}^{v_n-v_0}}\\ =\left|\frac{q_{v_n}}{\beta p_{v_n}}\right|\lim_{n\rightarrow\infty}\left|\frac{p_{v_n}}{q_{v_n}}\right|^{v_0}\cdot\lim_{n\rightarrow\infty}\frac{q_{v_n}^{v_0}}{q_{v_n}^{v_n}}=\left|\frac{q_{v_n}}{\beta p_{v_n}}\right|\cdot|\beta|^{v_0}\cdot0=0 \end{gather*} This contradicts inequality $(3)$. Hence we conclude that $\frac{1}{\beta}$ is also a Liouville number.
Can someone verify this solution? Please point out if there is any flaw in the proof and then I will try to fix that. Any help will be appreciated. Thanks in anticipation!