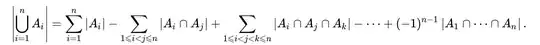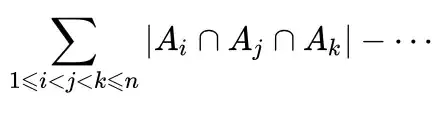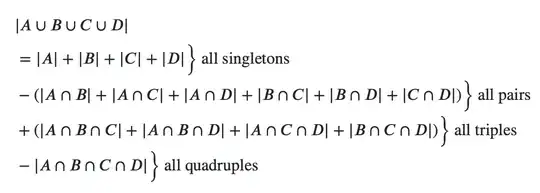0

I have a question regarding a later term in this formula from wiki:

Wiki Formula

The question is specifically regarding the $-$ minus sign in the following part of the formula:

Minus sign

Why are negative terms not appearing the the following answer? Specifically in the second to last line (all triples)? They are all being summed with $+$. Am I interpreting the formula or ellipsis incorrectly?

Solution to 4 terms

Andrés E. Caicedo
  • 81,687
Nick
  • 1,203
  • It seems to me that both the pairs and the quadruples have $-$ in front of them. – lulu Sep 01 '20 at 18:39
  • @lulu agreed, but why don't the triple have a $-$ in front of some. Isn't the ellipsis a continuation of the triples? – Nick Sep 01 '20 at 18:47
  • 1
    The signs ought to alternate (with the length of the terms), and, in the passage you quote, they do alternate. I don't see a problem. – lulu Sep 01 '20 at 19:05

1 Answers1

1

In the first formula you cited (the one from Wikipedia), each sum you see corresponds to a bracketed term such as "all singletons," "all pairs," "all triples," and so on. The minus sign you pointed out is meant to say that with each new sum, the sign alternates. To be a bit more concrete, if you write out the formula with $n=4$, it reads $$\begin{multline} \left| \bigcup_{i=1}^4 A_i \right| = \sum_{i=1}^4 |A_i| - \sum_{1 \leq i < j \leq 4} |A_i \cap A_j| + \sum_{1 \leq i < j < k \leq 4} |A_i \cap A_j \cap A_k| \\ - \sum_{1 \leq i < j < k < \ell \leq 4} |A_i \cap A_j \cap A_k \cap A_\ell|. \end{multline}$$ Notice that I wrote out the fourth sum here. It has a minus sign, since we're supposed to alternate the sign with each sum. Now what I claim is that if you actually write each term in each sum, you will obtain the second formula you cited, just with the letters $A_1, A_2, A_3, A_4$ in place of $A,B,C,D$. To better see this, take a look at the third sum: $$ \sum_{1 \leq i < j < k \leq 4} |A_i \cap A_j \cap A_k|. $$ This tells us to add a term for each triple of integers $(i,j,k)$ satisfying $1 \leq i < j < k \leq 4$. Start by listing these: $(1,2,3)$, $(1,2,4)$, and so on. Altogether, there are four such triples, and the sum becomes $$ |A_1 \cap A_2 \cap A_3| + |A_1 \cap A_2 \cap A_4| + |A_1 \cap A_3 \cap A_4| + |A_2 \cap A_3 \cap A_4|.$$ These are the same terms labeled "all triples" in the second formula, just with the different letters. If you've followed up to this point, you should be able to write out the other summations and see that the two formulas are the same. I think you'll find that the fourth minus sign does appear in the second formula, in front of the term $|A_1 \cap A_2 \cap A_3 \cap A_4|$.

nahp
  • 621
  • 3
  • 9