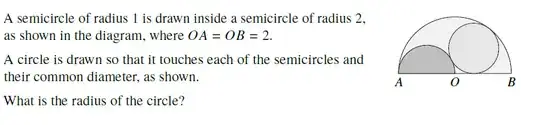Semicircle Question

Question

I need help with the question in the image. I just need someone to help by pointing me in the right direction. I don't want a full solution. I want to try to work out this question myself but I just need someone to direct me.

I was thinking if the question had something to do with joining the three points in the circle where the circle is touching the semicircles?

Or perhaps this question has something to do with similar triangles? I know that an angle subtended by an arc inside a semicircle is 90 degrees.

Answer 1

Hint: You may try using the tangent-secant version of the power of point theorem, remember that if two circles are tangent to each other (internally or externally), their centers and the point of tangency are collinear and draw all radii possible.

Answer 2

The hint:

Solve the following equation: $$\sqrt{(1+x)^2-x^2}=1+\sqrt{(2-x)^2-x^2},$$ where $x$ is a needed radius.

Answer 3

HINT

Try with an approach by Circular Inversion which leads to $r=\frac 8 9$.

Answer 4

Let the center of small semi-circle be C, point on the AB where circle touches touches is D, p denotes center of the circle, E is the point where circle touches bigger semi-circle. Le the circle touch the smaller semi-circle at T. Let the radius of the circle be $r$, then $$OP=2-r, OD=\sqrt{(2-r)^2-r^2}=\sqrt{4-4r}, CD=\sqrt{(1+r)^2-r^2}=\sqrt{2r+1}.$$ Finally, $$CD-OD=1 \implies \sqrt{1+2r}-\sqrt{4-4r}=1 \implies r=8/9.$$

Answer 5

Hint

Try to join all centres and points of contact.