What is $\mathbb{E}\!\left(X^2 \mid X + 2Y \right)$ if $X,Y \sim \mathcal{U}\left(\left[-1,1\right]\right)$ independently?

Question

$X$ and $Y$ are independent random variables of the uniform distribution on $\left[-1,1\right]$, $X,Y \sim \mathcal{U}\!\left(\left[-1,1\right]\right)$.

What is $\mathbb{E}\!\left(X^2 \mid X + 2Y \right)$?

My attempt:

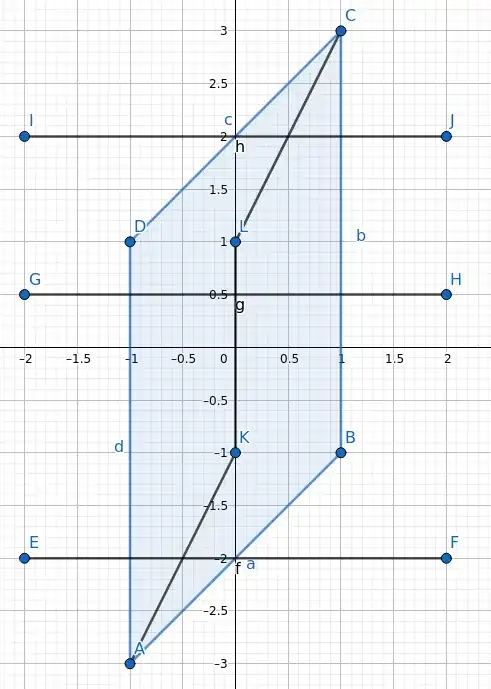
We need the joint pdf of $X$ and $X+2Y$ (as suggested). So we do a change of variables, let $W = X,~Z = X + 2Y$. This is a linear transformation, so the jacobian will be a constant. We need to find the image of the square $-1 \leq x, y \leq 1$ under this transformation. Since it is a linear transformation, the four edges of boundaries will be mapped to line segments. So we can find them by computing where the four corners of the square are mapped:

$$\begin{align} \left(x,y\right)&|\left(w,z\right)\\ (-1,-1) &| (-1, -3)\\ (-1,+1) &| (-1,+1)\\ (+1,+1) &| (+1,+3)\\ (+1,-1) &| (+1,-1) \end{align}$$

The image of the square is the parallelogram with vertices as above and in the picture below:

The joint density of $W$ and $Z$ will be uniform on this region, let A denote the interior of the parallelogram. Since it has area of 8, we can conclude

$f_{W,Z}\left(w,z\right) = \frac{1}{8}\unicode{x1D7D9}\left(\left(w,z\right) \in A\right) = \begin{cases} \frac{1}{8}, & \text{if $-1\leq w \leq 1,~-2+w\leq z\leq2+w$} \\ 0, & \text{otherwise} \end{cases}.$

The computations for $\mathbb{E}\left(X|X+2Y\right)$ and $\mathbb{E}\left(X^2|X+2Y\right)$ are below.

---

(for $\mathbb{E}\left(X|X+2Y\right)$, $Z = X + 2Y$)

Now we can figure out what $f_{X|Z}\left(x|z\right)$ is. We must consider three cases:

1. $-3 \leq z \leq -1$, given $Z = z$, $X$ is uniformly distributed between $-1$ and $z+2$. So $\mathbb{E}\!\left(X|Z=z\right) = \frac{-1+2+z}{2} = \frac{z}{2} + \frac{1}{2}$

2. $-1 \leq z \leq 1$, given $Z = z$, $X$ is uniformly distributed between $-1$ and $1$. So $\mathbb{E}\!\left(X|Z=z\right) = \frac{-1+1}{2} = 0$

3. $1 \leq z \leq 3$, given $Z = z$, $X$ is uniformly distributed between $1$ and $z-2$. So $\mathbb{E}\!\left(X|Z=z\right) = \frac{1-2+z}{2} = \frac{z}{2} - \frac{1}{2}$

Cases $1,2,3$ (with $0$ otherwise) gives us $\mathbb{E}\!\left(X|Z=z\right)$.

---

(for $\mathbb{E}\left(X^2|X+2Y\right)$, $Z = X + 2Y$)

We must consider three cases:

1. $-3 < z \leq -1$, given $Z = z$, $X$ is uniformly distributed between $-1$ and $z+2$ (so probability density function $f_{X|Z}(x|z) = \frac{1}{(z+2) - (-1)} = \frac{1}{z+3}$). So $\mathbb{E}\!\left(X^2|Z=z\right) = \int_{-1}^{z+2}x^2 \cdot \frac{1}{z+3}dx = \frac{1}{3} \cdot \frac{(z+2)^3+1}{z+3}$

2. $-1 \leq z \leq 1$, given $Z = z$, $X$ is uniformly distributed between $-1$ and $1$ (probability density function $f_{X|Z}(x|z) = \frac{1}{2}$). So $\mathbb{E}\!\left(X^2|Z=z\right) = \int_{-1}^{1}x^2 \cdot \frac{1}{2}dx = \frac{1}{3}$

3. $1 \leq z < 3$, given $Z = z$, $X$ is uniformly distributed between $1$ and $z-2$. So $\mathbb{E}\!\left(X^2|Z=z\right) = \int_1^{z-2}x^2\frac{1}{z-3}dx = \frac{1}{3}\cdot\frac{1}{z-3}\cdot\left((z-2)^3-1\right)$

Cases $1,2,3$ (with $0$ otherwise) gives us $\mathbb{E}\!\left(X^2|Z=z\right)$.

Answer 1

Observe that

• $X|(X+2Y = k) \sim \text{Unif}(-1,1)$ for $k\in[-1,1]$;
• $X|(X+2Y = k) \sim \text{Unif}(-1,2+k)$ for $k\in (-3,-1)$ and
• $X|(X+2Y = k) \sim \text{Unif}(k-2,1)$ for $k\in (1,3)$

Therefore,

• $\mathbb{E}(X^2|X+2Y = k) =\displaystyle\int_{-1}^1 \frac{1}{2}(x^2)dx = \frac{1}{3}$ for $k\in[-1,1]$;
• $\mathbb{E}(X^2|X+2Y = k) =\displaystyle\int_{-1}^{2+k} \frac{x^2}{3+k}dx = \frac{(2+k)^3+1}{3(3+k)}$ for $k\in (-3,-1)$ and
• $\mathbb{E}(X^2|X+2Y = k) =\displaystyle\int_{k-2}^{1} \frac{x^2}{3-k}dx = \frac{1-(k-2)^3}{3(3-k)}$ for $k\in[1,3]$

Answer 2

Define $h:\mathbb{R} \to \mathbb{R}$ such that $h(x)=\frac 1 3 \chi_{[-3,3]}$.

The claim is that $\mathbb{E}\left(X^2 | X + 2Y \right)=h(X+2Y)$.

---

Suppose $B \in \mathscr{B}([-3,3])$.

Let us prove $\int \chi_{B}(x+2y)x^2dx dy=\int \chi_{B}(x+2y)h(x+2y)dxdy$.

If $g(x,y)=(x+2y,x)$ then $|\det g (x,y)|=2$ and thus we have to prove $$\int_{[-3,3]\times [0,1]} \chi_{B}(z)x^2dz dx=\int_{[-3,3]\times [0,1]} \chi_{B}(z)h(z)dzdx$$

thanks to the change of variable.

Now $\int_{[-3,3]\times [0,1]} \chi_{B}(z)x^2dz dx=\mu(B)\frac 1 3$ and $\int_{[-3,3]\times [0,1]} \chi_{B}(z)h(z)dzdx=\int_{[-3,3]\times [0,1]} \chi_{B}(z)\frac 1 3 dzdx=\mu(B)\frac 1 3$ which conclude the proof.