1

My problem was like this

Find $u$ to minimize the following objective function :

$\left\| {y - Hu} \right\|_2^2 + {\lambda _1}\left\| u \right\|_2^{} + {\lambda _2}\left\| u \right\|_2^2$

Where ${\lambda _1},{\lambda _2} > 0$

Effort so far from taking the derivative

$ - 2{H^T}y + {H^T}Hu + 2{\lambda _2}u + {\lambda _1}\frac{{{u^T}}}{{\left\| u \right\|}}=0$

I dont know how to solve this equation for u ?

Royi
  • 10,050
Tuong Nguyen Minh
  • 363
  • Minimize it over what? If it is an open set taking the derivative and setting it equal to $0$ would give a list of candidates. If there is a boundary it has to be considered separately. – Conifold Aug 23 '20 at 03:44
  • Minimize over $u$ this is an unconstrained optimization problem with $H$ is a squared matrix – Tuong Nguyen Minh Aug 23 '20 at 04:42
  • So take the derivative (gradient) with respect to $u$ and find where it is $0$. – Conifold Aug 23 '20 at 04:44
  • I am not sure how to solve this equation $ - 2{H^T}y + {H^T}Hu + 2{\lambda _2}u + {\lambda _1}\frac{{{u^T}}}{{\left| u \right|}} = 0$ since it contain the term ${\left| u \right|}$ ? – Tuong Nguyen Minh Aug 23 '20 at 04:46
  • Shouldn't that $u^T$ be $u$? You can't add vectors to covectors. Then you have $\left({H^T}H + (2{\lambda _2} + \frac{\lambda _1}{\left| u \right|})I\right)u=2{H^T}y$ or $({H^T}H + \mu I)u=2{H^T}y$, where $\mu$ is an unknown constant. For each $\mu$ you can solve for $u$ and then see if it also satisfies $\mu=2{\lambda _2} + \frac{\lambda _1}{\left| u \right|}$. You may have to do numerical iteration until it matches. – Conifold Aug 23 '20 at 05:00
  • I agree with you there should not be a transpose on $u$. Also how can we now how to choose the value for $\mu $ since I do not know the range of $\mu $ ? – Tuong Nguyen Minh Aug 23 '20 at 06:37
  • 2
    You have a nonlinear equation $\mu-2{\lambda _2} - \frac{\lambda _1}{\left| ({H^T}H + \mu I)^{-1}2{H^T}y \right|}=0$, there are standard non-linear solvers that do such things. They usually require an initial guess, and if you do not have an idea as to its value you can try to graph the function on the right to see where it changes sign, roughly. There can be several solutions. – Conifold Aug 23 '20 at 07:55

1 Answers1

1

One way to solve this, in a large scale manner, would by using PD3O - A New Primal Dual Algorithm for Minimizing the Sum of Three Functions with a Linear Operator.

This is a 3 operators primal dual split method:

$$ \arg \min_{\boldsymbol{x}} \underbrace{\frac{1}{2} {\left\| \boldsymbol{A} \boldsymbol{x} - \boldsymbol{b} \right\|}_{2}^{2} }_{ f \left( \boldsymbol{x} \right) } + \underbrace{ {\lambda}_{1} {\left\| \boldsymbol{x} \right\|}_{2} }_{g \left( \boldsymbol{x} \right)} + \underbrace{ {\lambda}_{2} {\left\| \boldsymbol{x} \right\|}_{2}^{2} }_{ h \left( \boldsymbol{P} \boldsymbol{x} \right) } $$

The method, in general, requires the following:

  • $ {\nabla}_{\boldsymbol{x}} f \left( \boldsymbol{x} \right) = \boldsymbol{A}^{T} \left( \boldsymbol{A} \boldsymbol{x} - \boldsymbol{b} \right) $.
  • $ \operatorname{Prox}_{\lambda g \left( \cdot \right)} \left( \boldsymbol{y} \right) = \boldsymbol{y} \left( 1 - \frac{\lambda}{\max \left( {\left\| \boldsymbol{y} \right\|}_{2} , \lambda \right)} \right) $.
    See Closed Form Solution of $ \arg \min_{x} {\left\| x - y \right\|}_{2}^{2} + \lambda {\left\|x \right\|}_{2} $ - Tikhonov Regularized Least Squares.
  • $ \operatorname{Prox}_{\lambda h \left( \cdot \right)} \left( \boldsymbol{y} \right) = {\left( \boldsymbol{I} + \lambda \boldsymbol{I} \right)}^{-1} \boldsymbol{y} $.
    Due to the fact $ \boldsymbol{P} = \boldsymbol{I} $. This is basically a constant scaling of each element of $ \boldsymbol{y} $.

In the specific form of the problem above it will require not matrix decomposition or inversion.

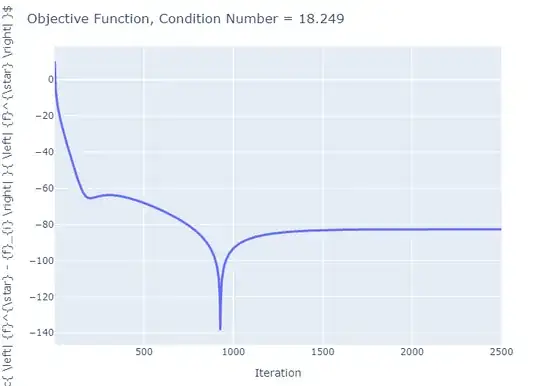
enter image description here

It is also pretty fast to converge (Case of $ \boldsymbol{A} \in \mathbb{R}^{500 \times 400} $) for the case above while the run time is also quite fast (Can be farther optimized).

The Julia code is available at my StackExchange Mathematics Q3800282 GitHub Repository (Look at the Mathematics\Q3800282 folder).

Royi
  • 10,050