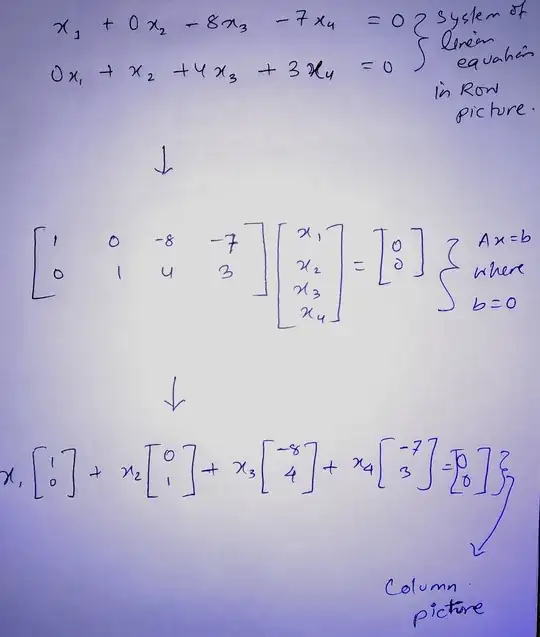1

I already read post this and this, but still I am not having clear understanding on parametric vector form.

I was reading a book Interactive linear algebra and found a problem where they used a parametric vector form for homogeneous case which I attached below.

enter image description here

They have taken a matrix in reduced row echelon form then they got system of equation from that. From system of equation they generated parametric form. I got how they deduce frist two equations x1 and x2. But they wrote more two lines which are x3 = x3 and x4 = x4. And seems like value of x3 and x4 could be anything.

My question is, how they got x3 = x3 and x4 = x4 ? Do we need to write mathematically free variable as, free variable = free variable?

And why do we need to write equations in parametric vector form, To find what are the vectors in system of linear equation exist?

One more confusion..

enter image description here

I wrote system of equation from above by myself, showed all three pictures. Row picture, matrix picture and column picture I learned from Dr.Gilbert Strang book. Shouldn't there be linear combination of 4 two-dimensional vectors (1, 0), (0, 1), (-8, 4) and (-7, 3)?

Also concept of span is bothering me very much. Does span relates to all possible solution set x or it relates to set of all linear combination of vectors that is all b's in case of Ax = b?

Btw, sorry for such a long question. But I had to use two image to make my question clear.

F.C. Akhi
  • 191

1 Answers1

1

Remember that (1,0), (0,1), (-8,4) and (-7,3) are not linearly independent, that is, you can express (-8,4) as -8*(1,0) + 4*(0,1) and (-7,3) as -7*(1,0) + 3*(0,1).

Answering your question, you need a parametric vector solution set because the system of equations that is provided to you is underconstrained, that is, the number of variables is greater than the number of equations. And so, you must express the variables x1 and x2 in terms of X3 and x4 (free variables).

G R Krishna Chand Avatar
  • 303
  • What if number of variables is less than number of equations? I remember, such case. And I didn't saw solving it using parametric form. What is going on then? – F.C. Akhi Aug 22 '20 at 16:17
  • Try thinking of simple extreme cases. For example, if you have $x_1 = 1$ and $x_1 = 2$ then it is obvious that $x_1$ can't both be 1 and 2 at the same time. So having more equations than variables will often result in no solutions. Unless there are redundant equations like 3 equations all being $x_1 = 1$. – dgadjov Aug 22 '20 at 16:41
  • Just consider that you are looking for the kernel of $A$, or more exactly for a basis of this kernel. – Jean Marie Aug 22 '20 at 16:57
  • @Jean Marie What do you mean by kernel of A? – F.C. Akhi Aug 23 '20 at 10:26
  • @AsAnExerciseProve So you meant if my equations were not redundant , then I will end up with no solution? And If equations were redundant then I will have unique solutions? – F.C. Akhi Aug 23 '20 at 10:29
  • I mean that if $A$ is $n \times p$ (n lines and p columns), the set of $X \in \mathbb{R^p}$ such that $AX=0$ is a subspace of $\mathbb{R^p}$ which is traditionally called the kernel of $A$. It is one of the most important concept in linear algebra. – Jean Marie Aug 23 '20 at 21:23