Hint:
Use this fact:
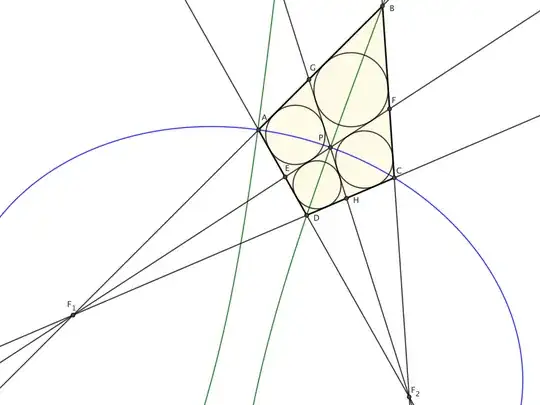
ُThe center of four circle I, J, K and L are on a circle (M) concentric with inscribed circle N at O and Lines AO, BO, CO and DO which connect vertices of quadrilateral to the center (O) of inscribed circle.
Now follow this rule:
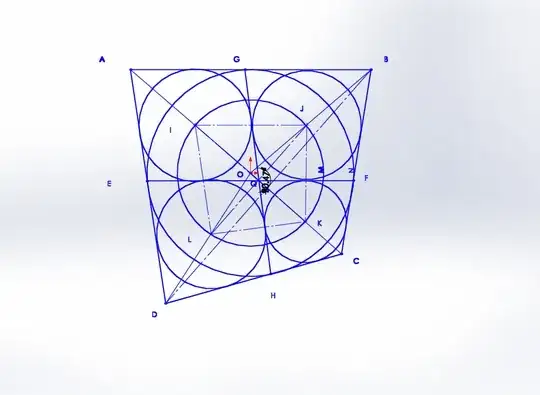
1- Draw AO. BO, CO and DO.
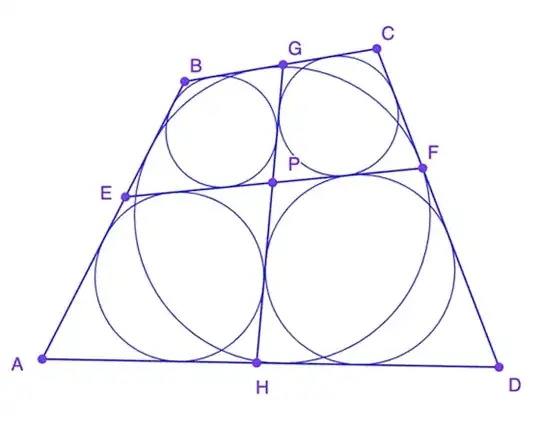
2-draw AC and BD, they intersect on P.
3-Connect OP.
4- find the midpoint of OP and mark it as Q. Q is the intersection
of EF and GH (in your figure P).
5- Draw a line parallel with BD, it intersect BO and DO on J and L respectively.these are the center of two opposite circles.They also define the measure of the radius (M).
6- Draw circle (M), it intersect AO and CO on I and K respectively. these are the centers of other two opposite circles.
7- Draw four cicles.
8- draw common tangents of adjacent circles, they will intersect on Q( in your figure P) and you get EF and GH.
The reason for taking Q as the midpoint of OP is that if equilateral is regular, points P and O and Q will be coincident. If it is not regular , they will have a distance like OP and the intersection of common tangents locates on its midpoint Q.