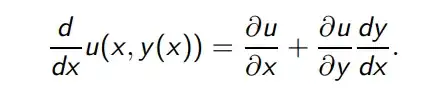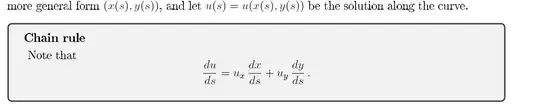2

enter image description here

For the part $\frac{\partial u}{\partial x}$, do we do $\frac{\partial u(x,y)}{\partial x}$ first, then evaluate at the point $(x,y)=(x,y(x))?$

enter image description here

For the part $u_{x}$, do we do $\frac{\partial u(x,y)}{\partial x}$ first, then evaluate at the point $(x,y)=(x(s),y(s))?$

I was bit confused with different notations. If we are given derivative notation without specify the order of evalution, is there any general rules to follow?

000000000
  • 497
  • For the first one, it means that the derivative of $u$ evaluate at some point $\bar{x}$ is $$ \frac{du}{dx}(\bar{x}) = \frac{\partial u}{\partial x}(\bar{x},y(\bar{x})) + \frac{\partial u}{\partial y}(\bar{x},y(\bar{x})) \frac{dy}{dx}(\bar{x}) $$ Can you get the secpond rule? – Marc Dinh Aug 05 '20 at 13:09
  • 2
    I should also say that the formula use an abuse of notation that maybe confusing at first. – Marc Dinh Aug 05 '20 at 13:15
  • Yeah, I think I get the idea. Sometimes I feel confused if there is abuse of notation. – 000000000 Aug 05 '20 at 13:30
  • 1
    Yes, notation is very confusing, and it's just one of those things you have to get used to with practice. Here is a pretty lengthy answer I wrote a while back regarding various ways of writing down the notation. Perhaps a few other examples might help: see this answer which deals with expressions encountered in Lagrangian mechanics, but also very relevant here, and also partial derivatives in the context of implicit differentiation. – peek-a-boo Aug 07 '20 at 23:36

0 Answers0