Given two circles externaly tangent to each other and the common tangent line. Draw a third tangent circle.

Question

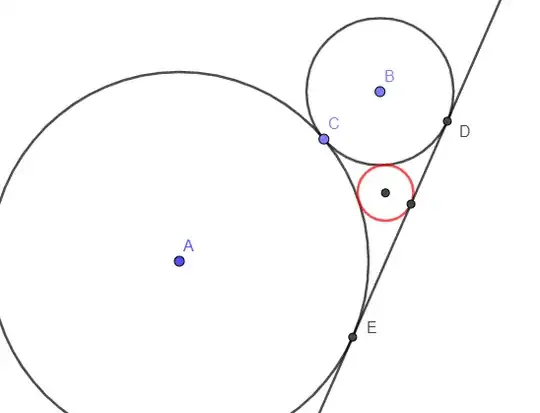
We are given $\Gamma_A$ centered at $A$ and $\Gamma_B$ centered at $B$ tangent to each other externally at $C$. Line $DE$ is one common tangent to both not through $C$.

Is there a nice way to draw the red circle externally tangent to both and to line $DE$ without using the complete apollonius solution for the $CCL$? Are there any nice symetries in this problem?

I only saw the homotheties which would mean a few tangency points would be colinear and of course Monge-D'Alembert theorem implies one more colinearity between the tangency points and the exterior homothetic center

score 3 · Accepted Answer · answered Jul 30 '20 at 12:10

3

Use inversion with center at $O$ (touching point of given circle) and arbitrary radius (I've choose $r$ = distance of $O$ to given line for ease). So we are looking at inversion with respect to red circle.

Mark all given objects with dots.

Now both circles goes to parallel and line goes to a circle touching both lines. Now the image of a circle we are searching (blue) is a circle touching these twi parallels and circle between them and on a picture is green circle (and it is easy to draw it). Now map this green and you get blue circle, the one we are searching.

answered Jul 30 '20 at 12:10

nonuser

91,557

this is nice one! – Math Lover Jul 30 '20 at 12:18
this is a nice one still I'm having it bad drawing the green circle. I thought the line joining it with the center of the inversion one would be parallel to the others. – hellofriends Jul 30 '20 at 12:27
1

Yes, draw that line and where it cuts black circle is touching point of green with black. Radius of green is same as black. – nonuser Jul 30 '20 at 12:33
lol i didn't draw the black one, sorry – hellofriends Jul 30 '20 at 12:38

score 2 · Answer 2 · answered Jul 30 '20 at 11:54

2

If the radius of the circle $A$ is $a$ and of $B$ is $b$, $DE = 2\sqrt{ab}$.

Say, the center of red circle is $O$, the radius $= r$, and parallel line to $DE$ through $O$ meets $AE$ at $A'$ and $BD$ at $B'$.

$DE = OA' + OB'$
or, $2\sqrt{ab} = 2\sqrt{ar} + 2\sqrt{br}$
or, $r = \frac{ab}{a+b+2\sqrt{ab}}$

Now that we know the value of $r$, draw A'B' parallel line to $DE$ at a distance $r$.

Use a compass to draw an arc from center $A$ with radius $a+r$. Wherever it cuts the line $A'B'$ is point $O$, the center of the red circle. Now you can draw the circle of radius $r$ from the center.

answered Jul 30 '20 at 11:54

Math Lover

52,200

Yes, but you don't know what $a$ and $b$ are. And how do you construct $r$ from that formula? – nonuser Jul 30 '20 at 12:11
It says two given circles so I assume you know their radius. – Math Lover Jul 30 '20 at 12:16
Unforunately you can't. If I draw a circle with radius $r$, you don't know what it is unless I told you. – nonuser Jul 30 '20 at 12:28
If you do not know $a$ and $b$ then I agree but if you know, this works. – Math Lover Jul 30 '20 at 12:35
1

Yes, I agree, but still, how you draw $r$ exactly if say $a=\pi$ and $b=e$. – nonuser Jul 30 '20 at 12:37
Anway, nice work +1 – nonuser Jul 30 '20 at 12:40
If we know a and b, we can find $r$. That is what I found in my solution. – Math Lover Jul 30 '20 at 12:42
1

Btw I see your point about $\pi$, $e$ :) knowing will be one thing and drawing will be another as I do not know it exactly! – Math Lover Jul 30 '20 at 12:49
How do you get the formulae for DE, OA' and OB' ? – M.M May 29 '24 at 13:29

score 0 · Answer 3 · answered Aug 08 '20 at 21:16

I did it. It uses a generalization of a result involving a chain of tangent circles that look like this:

Given the following tangent circles chain to draw the next circle of the chain

To a degenerate case. Anyway here it is:

Let the two given circles $\Gamma _A$ and $\Gamma _B$ touch the line $\ell$ at points $A \in \Gamma _A$ and $B \in \Gamma _B$. Take $C$ to be the antipode of $A$ on $\Gamma _A$ and $D$ the antipode of $B$ on $\Gamma _B$.

Draw the tangent line from $D$ to $\Gamma _A$ (there are two tangent lines, right? Take the one such that the contact point $T$ is in the small region between $\Gamma _A$ and $\Gamma _B$).

Take $G = CT \cap \ell$. To end it just draw the perpendicular bissector of $GT$ and let it meet with a line perpendicular to $\ell$ through $G$ to get the center $O$ of the third circle and draw it centered at $O$ passing through $G$.

Given two circles externaly tangent to each other and the common tangent line. Draw a third tangent circle.

3 Answers3