3D Parametric Equation changing over time

Question

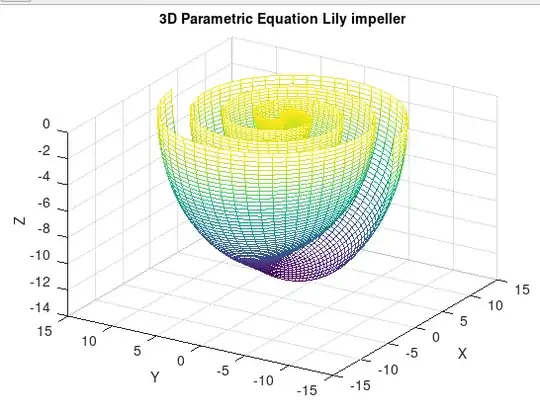
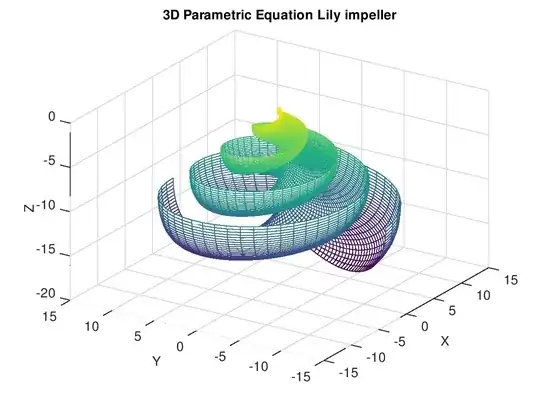
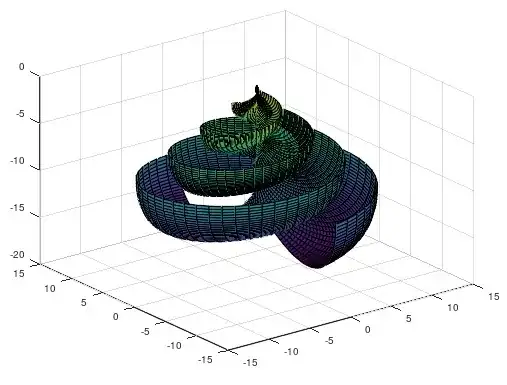
I can create a 3D Parametric Equation of a spiral but I'm having trouble getting the angle of "decent" to also change over time.

$$x=u\sin(u)\cos(v)$$ $$y=u\cos(u)\cos(v)$$ $$z=-u\sin(v)$$

The Octave code I have so far seems close, I'm just not sure how to "tweak" it. The image it creates is:

clc
close all
clear all
u=linspace(0,4pi,100);
v=linspace(0,pi,100);
[u,v]=meshgrid(u,v);
x=u.sin(u).cos(v);
y=u.cos(u).cos(v);
z=-u.sin(v);
figure(1)
mesh(x,y,z);
view([-57,32])
h=gca; 
get(h,'FontSize') 
set(h,'FontSize',14)
xlabel('X','fontSize',14);
ylabel('Y','fontSize',14);
zlabel('Z','fontsize',14);
title('3D Parametric Equation Lily impeller','fontsize',14)
fh = figure(1);
set(fh, 'color', 'white'); 

The image I'm trying to recreate is the Lily Impeller and how it's created/growth pattern takes shape over time.

Here's a video of what I'm trying to model/animate the growth pattern of. https://youtu.be/by0JhirtO-0?t=224

I was thinking that the descending curves in the $-Z$ direction may need to be at a $60^\circ$ angle or so but I couldn't come up with a way of how to do this.

Answer 1

As the curve moves radially out from $(0,0)$ reduce $z$ at a $60^{\circ}$ angle.

z=-u.*sin(v) .-  sin(60/180 * pi)*(sqrt((x).^2 + (y).^2));

This subtracts a $60^{\circ}$ angle cone from the $z$ value.

surf(x,y,z)

You can adjust the angle and scale to match the image / your taste.

Depending on how you define the angle:

z=-u.*sin(v) .-  cos(60/180 * pi)*(sqrt((x).^2 + (y).^2));

---

clc
close all
clear all
u=linspace(0,4pi,100);
v=linspace(0,pi,100);
[u,v]=meshgrid(u,v);
x=u.sin(u).cos(v);
y=u.cos(u).cos(v);
z=-u.sin(v) .-  sin(60/180 * pi)*(sqrt((x).^2 + (y).^2));
figure(1)
mesh(x,y,z);
view([-57,32])
h=gca; 
get(h,'FontSize') 
set(h,'FontSize',14)
xlabel('X','fontSize',14);
ylabel('Y','fontSize',14);
zlabel('Z','fontsize',14);
title('3D Parametric Equation Lily impeller','fontsize',14)
fh = figure(1);
set(fh, 'color', 'white');