I am having trouble with the general definition of Chain homology. Given an Abelian category $\textbf{A}$, I have defined the category of Chain Complexes $\text{Ch}_\bullet(\textbf{A})$ as usual. Moreover, I have defined subobjects and quotient objects as equivalence classes of monomorphisms and epimorphisms. In the special case where $f:X\to Y$ is a monomorphism, it gives rise to a quotient object $Y/X$ of $Y$ as the equivalence class of $\text{coker}(f)$.
In the case of the Chain Homology, it is supposedly defined as : $$H_n(C)=\ker(\partial_n)/\text{Im}(\partial_{n+1}).$$
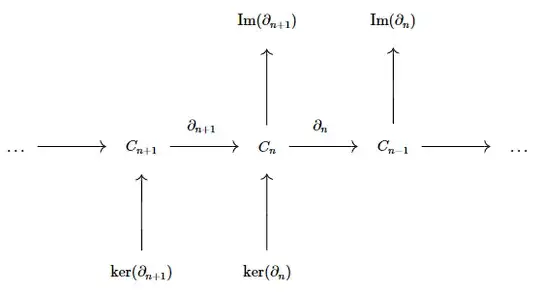
Now, if I consider the following diagram, I cannot put things all together :
The map $\ker(\partial_n)\to\text{Im}(\partial_{n+1})$ is the wrong way around to consider its cokernel. In fact, it has no reason to be either monic or epic...
What am I doing wrong ? Could someone explain to me the correct definition ? I cannot find anything else than the nLab article about it...