Surgery presentations
It is well known that any orientable closed 3-manifold $M$ has a surgery presentation, i.e. can be obtained by doing surgery on $\mathbb{S}^3$ on a link $L$. We can also construct a surgery diagram where the link has all unknotted components and two components are either unlinked or an Hopf link. Also we can require that if an unknot component $U_i$ is unlinked from $U_j$ for any $j\neq i$ then $U_i$ is unlinked from $\{U_j\}_{j\neq i}$. Therefore we can construct a surgery graph for $M$, where each unknot is a vertex and we have an edge between two vertices if they are linked.
Graph manifolds
These 3-manifolds are obtained by plumbing on a labelled graph. Given a graph we construct a $\mathbb{D}^2$ bundle over $\mathbb{S}^2$ for each vertex (with Euler class given by the label) and then we plumb* two of them whenever the two vertices are connected by an edge. In this way we get a 4-manifold with boundary $X$, the resulting graph manifold is the boundary $\partial X$.
Confusion
The $\mathbb{D}^2$ bundle over $\mathbb{S}^2$ of Euler characteristic $n$ has a surgery presentation given by the unknot labelled with $n$. Plumbing corresponds to link two unknots like the Hopf link, at least if we are plumbing on a graph which is a tree. Otherwise when we plumb on an edge that creates a cycle in the graph, then we have to link the two unknots like an Hopf like as before but also add another unknot like in this picture.
(Before)
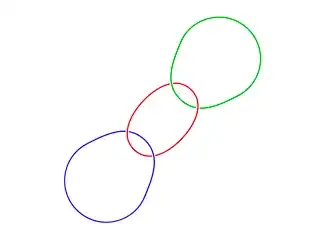
Now we can use Kirby moves to obtain from this a surgery graph with the properties mentioned above.
It seems to me that every 3-manifold that has a tree as surgery graph must be a graph manifold. In general, if the graph is not a tree maybe we will get a graph manifold, maybe not. How can we spot from the surgery graph of $M$ if it is a graph manifold? Does these kind of graphs have some particular feature?
*plumbing means identify two trivialized open set of the form $\mathbb{D}^2\times \mathbb{D}^2$by exchanging fiber with base.
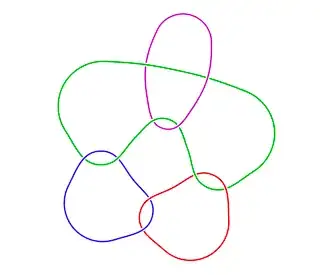
The "confusing" (to me) part I wrote to motivate the problem tries to explain that apparently is not is not simple to draw a surgery graph that yields a non-graph manifold (graph manifolds are a lot).
– Overflowian Jun 10 '20 at 21:25