Prove that $\sum_{\mathrm{cyc}} \frac{214x^4}{133x^3 + 81y^3} \ge x + y + z$ for $x, y, z > 0$

Question

Problem. Let $x, y, z > 0$. Prove that $$\frac{214x^4}{133x^3 + 81y^3} + \frac{214y^4}{133y^3 + 81z^3} + \frac{214z^4}{133z^3 + 81x^3} \ge x+y+z.$$

It is verified by Mathematica. The inequality holds with equality if $x = y = z$. When $x = \frac{121}{84}, y = \frac{43}{66}$ and $z = 1$, $\mathrm{LHS} - \mathrm{RHS} \approx 0.000005327884220$.

It is a stronger version of the inequality in this link: Olympiad Inequality $\sum\limits_{cyc} \frac{x^4}{8x^3+5y^3} \geqslant \frac{x+y+z}{13}$

They can be written as (for $k = \frac{8}{5}$ and $k = \frac{133}{81} \approx 1.641975$, respectively) $$\frac{x^4}{kx^3+y^3} + \frac{y^4}{ky^3 + z^3} + \frac{z^4}{kz^3 + x^3} \ge \frac{x+y+z}{k+1}.$$

The best constant $k$ is approximately $1.64199$ (see the comment by @Colescu in the link above).

I can prove the inequality of $k = \frac{8}{5}$ by the Buffalo Way. Several months ago, I tried to prove the inequality of $k = \frac{133}{81}$ by the Buffalo Way without success. However, I think that the Buffalo Way may work but just I have not found the way.

Any comments and solutions are welcome.

Answer 1

We can reduce a degree of this inequality.

Indeed, by C-S we obtain: $$\sum_{cyc}\frac{x^4}{133x^3+81y^3}=\sum_{cyc}\frac{x^4(200x-57y+154z)^2}{(133x^3+81y^3)(200x-57y+154z)^2}\geq$$ $$\geq\frac{\left(\sum\limits_{cyc}(200x^3-57x^2y+154x^2z)\right)^2}{\sum\limits_{cyc}(133x^3+81y^3)(200x-57y+154z)^2}$$ and it's enough to prove that: $$214\left(\sum\limits_{cyc}(200x^3-57x^2y+154x^2z)\right)^2\geq(x+y+z)\sum\limits_{cyc}(133x^3+81y^3)(200x-57y+154z)^2,$$ which is true, but BW does not help here and I have no a proof by hand.

Answer 2

Here I present the computer-generated Buffalo Way solution. I didn't think the solution to be this ugly when I coded this, but it happens.

We want to prove $$872613 x^{7}y^{3} + 531441 x^{7}z^{3} + 872613 x^{6}y^{4} - 1432809 x^{6}y^{3}z - 872613 x^{6}yz^{3} - 872613 x^{6}z^{4} - 872613 x^{4}y^{6} + 901368 x^{4}y^{3}z^{3} + 872613 x^{4}z^{6} + 531441 x^{3}y^{7} - 872613 x^{3}y^{6}z + 901368 x^{3}y^{4}z^{3} + 901368 x^{3}y^{3}z^{4} - 1432809 x^{3}yz^{6} + 872613 x^{3}z^{7} - 1432809 xy^{6}z^{3} - 872613 xy^{3}z^{6} + 872613 y^{7}z^{3} + 872613 y^{6}z^{4} - 872613 y^{4}z^{6} + 531441 y^{3}z^{7}$$ is positive.

The Buffalo Way method helps.

This polynomial is symmetric.

Let $x = \min\{x, y, z\}$, $y = x + a$, $z = x + b$.

Substitution gives $$\left(3016116 a^{2} - 3016116 a b + 3016116 b^{2}\right) x^{8} + \left(7540290 a^{3} + 24659883 a^{2} b - 23151825 a b^{2} + 7540290 b^{3}\right) x^{7} + \left(15461928 a^{4} + 51247485 a^{3} b + 25272972 a^{2} b^{2} - 60313167 a b^{3} + 15461928 b^{4}\right) x^{6} + \left(15652602 a^{5} + 63883971 a^{4} b + 75012399 a^{3} b^{2} - 33150789 a^{2} b^{3} - 49375413 a b^{4} + 15652602 b^{5}\right) x^{5} + \left(7522956 a^{6} + 44891091 a^{5} b + 95298039 a^{4} b^{2} + 11145762 a^{3} b^{3} - 46208151 a^{2} b^{4} - 11765817 a b^{5} + 7522956 b^{6}\right) x^{4} + \left(1404054 a^{7} + 16644285 a^{6} b + 60598125 a^{5} b^{2} + 44855208 a^{4} b^{3} - 28491912 a^{3} b^{4} - 13640319 a^{2} b^{5} + 3619161 a b^{6} + 1404054 b^{7}\right) x^{3} + \left(2617839 a^{7} b + 19262124 a^{6} b^{2} + 30670731 a^{5} b^{3} - 15018129 a^{3} b^{5} + 3306744 a^{2} b^{6} + 1594323 a b^{7}\right) x^{2} + \left(2617839 a^{7} b^{2} + 8165934 a^{6} b^{3} + 5235678 a^{5} b^{4} - 5235678 a^{4} b^{5} - 642978 a^{3} b^{6} + 1594323 a^{2} b^{7}\right) x + 872613 a^{7} b^{3} + 872613 a^{6} b^{4} - 872613 a^{4} b^{6} + 531441 a^{3} b^{7}$$

If we let $X = \frac{x}{\sqrt{a}\sqrt{b}}$,

We split into $58$ cases.

(1) For ${a}/{b}$ in range $\left[0.0, 0.4304\right]$, the polynomial is larger than $$\left(5289724 X^{8} + 9721601 X^{7} - 6472990 X^{6} - 27945512 X^{5} - 15542184 X^{4} + 13520031 X^{3} + 19931661 X^{2} + 8919859 X + 1378640\right)\left(\sqrt{a}\sqrt{b}\right)^{10}$$, which is positive.

(2) For ${a}/{b}$ in range $\left[0.4304, 0.4338\right]$, the polynomial is larger than $$\left(5245055 X^{8} + 9635887 X^{7} - 6470872 X^{6} - 27446186 X^{5} - 15442001 X^{4} + 13309502 X^{3} + 19625777 X^{2} + 8769605 X + 1355267\right)\left(\sqrt{a}\sqrt{b}\right)^{10}$$, which is positive.

(3) For ${a}/{b}$ in range $\left[0.4338, 0.4356\right]$, the polynomial is larger than $$\left(5221753 X^{8} + 9592263 X^{7} - 6456145 X^{6} - 27258913 X^{5} - 15339842 X^{4} + 13209802 X^{3} + 19470823 X^{2} + 8692567 X + 1343224\right)\left(\sqrt{a}\sqrt{b}\right)^{10}$$, which is positive.

(4) For ${a}/{b}$ in range $\left[0.4356, 0.4367\right]$, the polynomial is larger than $$\left(5207630 X^{8} + 9566190 X^{7} - 6442823 X^{6} - 27149048 X^{5} - 15272265 X^{4} + 13152771 X^{3} + 19378452 X^{2} + 8646323 X + 1335975\right)\left(\sqrt{a}\sqrt{b}\right)^{10}$$, which is positive.

The 5-58 cases are put in the link below. https://sagecell.sagemath.org/?q=vckhdl

Therefore we conclude that the polynomial is positive.

Answer 3

$\color{green}{\textbf{Version of 01.04.24. Common way.}}$

$\color{brown}{\;\textbf{1. Cubic in the specific form.}}$

The equation $$\dfrac{3t}{4t^3+d}=c^2,\qquad c>0,\quad c^3d\in[0,1]\tag{1.1}$$ can be solved via the trigonometric form: $$\dfrac{3ct}{4(ct)^3+c^3d}=1,\quad 3ct-4(ct)^3=c^3d,\quad \sin(3\arcsin(ct))=c^3d,$$ $$\mathbf{t_k=\dfrac1c\,sin\;\dfrac{2\pi k+\arcsin(c^3d)}3},\qquad k=0,1,2.\tag{1.2}$$ Since $\;c^3d\in[0,1],\;$ then $\;\arcsin(c^3d)\in\left[0,\dfrac\pi2\right],\;$

$$t_0=\dfrac1c\,\sin\;\dfrac{\arcsin(c^3d)}3\in\left[0,\dfrac1{2c}\right];\tag{1.3}$$ $$t_1=\dfrac1c\,\sin\;\dfrac{2\pi+\arcsin(c^3d)}3 =\dfrac1c\,\sin\;\dfrac{\pi-\arcsin(c^3d)}3\in\left[\dfrac1{2c},\dfrac{\sqrt3}{2c}\right];\tag{1.4}$$ $$t_2=\dfrac1c\,\sin\;\dfrac{4\pi+\arcsin(c^3d)}3=-\dfrac1c\,\sin\;\dfrac{\pi+\arcsin(c^3d)}3\in\left[-\dfrac{\sqrt3}{2c}, -\dfrac1{c},\right].\tag{1.5}$$

$\color{brown}{\textbf{2. The main areas.}}$

Taking in account the rotational symmetry of the given inequality $$\dfrac{x^4}{133x^3+81y^3}+\dfrac{y^4}{133y^3+81z^3}+\dfrac{z^4}{133z^3+81x^3}\ge\dfrac{x+y+z}{214},\tag{2.1}$$ we can WLOG assume $\;x\;$ the greatest one of the unknowns $\;\{x, y, z\}.\;$

Then it suffices to consider two main cases (areas):

$A. \quad 0\le z\le y\le x.$

$B. \quad 0\le y\le z\le x.$

$\color{brown}{\textbf{3. Edges.}}$

$\color{teal}{\textbf{3a. Edges, case A.}}$

Let $\;\color{teal}{\mathbf{\;z=0,\; 0<y\le x.\;}}$ Then inequality ($1.1$) takes a form of $$\dfrac{x^4}{133x^3+81y^3} +\dfrac{y^4}{133y^3}\ge\dfrac{x+y}{214}.$$ Substitution $u=\dfrac yx\in[0,1]$ presents it in the form of $L(u)\ge0,$ where $$L(u)=\dfrac1{133+81u^3}+\dfrac1{133}u-\dfrac{1+u}{214} =\dfrac{133\cdot214+214u(133+81u^3)-133(1+u)(133+81u^3)}{133\cdot214(133+81u^3)}$$ $$=\dfrac{81(81u^4-133u^3+133u+133)}{133\cdot214(133+81u^3)} =\dfrac{81(81u^4+133u(1-u^2)+133)}{133\cdot214(133+81u^3)}\ge 0.$$

The case is proven.

$\color{teal}{\textbf{3b. Edges, case B.}}$

Let $\color{teal}{\mathbf{\;y=0,\;0<z\le x.\;}}$ Then inequality ($1.1$) takes a form of $$\dfrac{x^4}{133x^3}+\dfrac{z^4}{133z^3+81x^3}\ge\dfrac{x+z}{214}.$$ Substitution $u=\dfrac zx\in[0,1]$ presents it in the form of $L(u)\ge0,$ where $$L(u)=\dfrac1{133}+\dfrac{u^4}{81+133u^3}-\dfrac{1+u}{214} =\dfrac{214(81+133u^3)+133\cdot214u^4-133(1+u)(81+133u^3)}{81\cdot214(81+133u^3)}$$ $$=\dfrac{133u^4+133u^3-133u+81}{214(81+133u^3)} =\dfrac{532u^4+532u^3-532u+324}{4\cdot214(81+133u^3)} =\dfrac{(14-23u^2)^2+3u^4+532u^3+(644u^2-532u+128)}{856(81+133u^3)}\ge0,$$ The case is proven.

Therefore, inequality ($2.1$) $\color{green}{\textbf{is proven at the bounds of the given area.}}$

$\color{brown}{\textbf{4. Substitutions.}}$

In the case "A", $\quad \color{teal}{\mathbf{0<z\le y\le x.}}$

Substitutions $$u=\dfrac yx\in[0,1],\quad v=\dfrac zy\in[0,1],\quad w=\dfrac xz=\dfrac1{uv}\in[1,\infty),\tag{4.1}$$ lead to presentation of the given inequality in the form of $$\dfrac{1}{133+81u^3}-\dfrac1{214}+u\left(\dfrac{1}{133+81v^3}-\dfrac1{214}\right)+uv\left(\dfrac1{133+81w^3}-\dfrac1{214}\right) \ge 0.\tag{4.2}$$

In the case "B", $\quad \color{teal}{\mathbf{0<y\le z\le x.}}$

Substitutions $$u=\dfrac zy\in[1,\infty],\quad v=\dfrac xz\in[1,\infty],\quad w=\dfrac yx=\dfrac1{uv}\in[0,1],\tag{4.3}$$ lead to presentation of the given inequality in the form of $$\dfrac{1}{133+81w^3}-\dfrac1{214}+\dfrac1{uv}\left(\dfrac{1}{133+81u^3}-\dfrac1{214}\right)+\dfrac1v\,\left(\dfrac1{133+81v^3}-\dfrac1{214}\right) \ge 0.\tag{4.4}$$ Both ($\text{4.2}$) and ($\text{4.4}$) can be written in the form of $$\dfrac1{uv}\,\dfrac{1-u^3}{133+81u^3}+\dfrac1v\,\dfrac{1-v^3}{133+81v^3}+\dfrac{1-w^3}{133+81w^3}\ge 0.\tag{4.5}$$

At the same time, the constraints ($\text{4.1}$) and ($\text{4.3}$) are specific ones.

Let $$\begin{cases} P(t)=\dfrac{1-t^3}{133+81t^3},\\[4pt] Q(t)=-P'(t)=\dfrac{642t^2}{(133+81t^3)^2},\\[4pt] R(t)= P(t)+tQ(t)=\dfrac{-81t^6+590t^3+133}{(81t^3 + 133)^2}, \tag{4.6}\end{cases}$$ then (${4.5}$) takes the form of $\;f(u,v)\ge0,\;$ where $$f(u,v)=P\left(\dfrac1{uv}\right)+\dfrac1v\left(P(v)+\dfrac1u\, P(u)\right).\tag{4.7}$$

$\color{brown}{\textbf{5. Inner stationary points.}}$

$\color{teal}{\textbf{5.1. Algebraic system.}}$

Stationary points can be defined from the system $\;f'_u=f'_v=0,\;$ or $$\begin{cases} P'\left(\dfrac1{uv}\right)\left(-\dfrac1{u^2v}\right)+\dfrac1v\left(-\dfrac1{u^2}\right)P(u)+\dfrac1{uv}\,P'(u)=0\\[4pt] P'\left(\dfrac1{uv}\right)\left(-\dfrac1{uv^2}\right)-\dfrac1{v^2}\left(P(v)+\dfrac1uP(u)\right)+\dfrac1vP'(v)=0, \end{cases}$$ $$\begin{cases} Q(w)-P(u)-uQ(u)=0\\[4pt] Q(w)-P(u)-uP(v)-uvQ(v)=0\\[4pt] uvw=1 \end{cases}\Rightarrow \begin{cases} R(u)=Q(w)\\[4pt] R(v)=Q(u)\\[4pt] uvw=1 \end{cases}\tag{5.1}$$

$\color{teal}{\textbf{5.2. The inequality transformation.}}$

Taking in account the equalities $(4.6),(4.7),(5.1)$ in the form of $$P(t)=R(t)-tQ(t),\quad R(u)=Q(w),\quad R(v)=Q(u),\quad uvw=1,$$ the inequality $$wf(u,v,w)=P(w)+w(P(u)+uP(v))\ge0$$ can be presented in a form of $$R(w)-wQ(w)+w\big(R(u)-uQ(u)+uR(v)-uvQ(v)\big)\ge0,$$ $$R(w)+w\big(R(u)-Q(w)\big)+uw\big(R(v)-Q(u)\big)-uvwQ(v)\ge0,$$ or $$R(w)-Q(v)\ge0.\tag{5.2}$$

$\color{brown}{\textbf{6. Explicit form of the inverse functions.}}$

$\color{teal}{\textbf{6.1. Inversion of $Q(t).$}}$

Function $Q(t)$ can be presented in the form of $$Q(t)=\dfrac{642t^2}{(133+81t^3)^2}=\dfrac{3424}{19683}\left(\dfrac{3t}{\dfrac{532}{81}+4t^3}\right)^2.\tag{6.1}$$

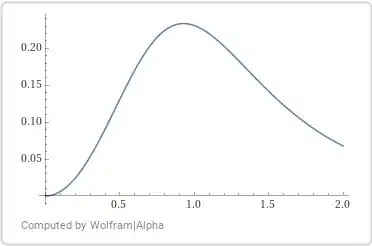
Then

• $Q(0)=0;$
• $\;\lim\limits_{t\to\infty}Q(t)=0;$
• $\;\dfrac{\text d}{\text dt}\dfrac{t}{133+81t^3}=\dfrac{133-162t^3}{(133+81t^3)^2},\\$
• $\max Q(t)=Q_m=\dfrac{428}{3591}\,\sqrt[\large3]{\dfrac2{1197}}\approx0.014142960\;$ at $\;t_m=\sqrt[\large3]{\dfrac{133}{162}}\approx0.936365798.$
• $Q(t)\;$ increases at $\;t\in[0,t_m];$
• $Q(t)\;$ decreases at $\;t\in[t_m,\infty].$

Taking in account $(1.1)-(1.2),$ inverse function $\;Q^{-1}(q)\;$ finally is $$\theta(k,q)=\sqrt[\large4]{\dfrac{3424}{3^9q}} \sin\left(\dfrac13\left(2\pi k+\arcsin\left(4788\left(\dfrac{3q}{3424}\right)^{\large\frac34}\right)\right)\right),\quad k=0,1.\tag{6.2}$$

Note that, in accordance with $(1.5),\quad\theta(2,q)<0.$

Therefore, there are two branches of the inverse function $Q^{-1}(q):$

• "zero" branch $\;\theta(0,q),\quad q\in\left(0,Q_m\right],\quad\theta(0,q)\in[0,\tau_m],\;$ and
• "first" branch $\;\theta(1,q),\quad q\in\left(0,Q_m\right],\quad \theta(1,q)\in[\tau_m,\infty].$

Easily to check, that

• $Q(\theta(k,q))=q,\quad q\in(0,\infty);$
• $\theta(0,Q(t))=t,\quad t t\in[0,t_m];$
• $\theta(1,Q(t))=t,\quad t\in[t_m,\infty].$

$\color{teal}{\textbf{6.2. Inversion of $R(t).$}}$

Function $R(t)$ can be presented in the form of $$R(t)=\dfrac{133+590t^3-81t^6}{(133+81t^3)^2}=\dfrac{457}{32319}-\dfrac1{6916266}\left(\dfrac{85386}{133+81t^3}-428\right)^2.\tag{6.3}$$

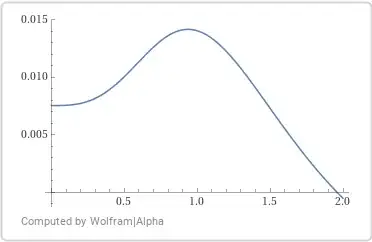
Easily to see, that

• $R(0)=\dfrac1{133}\approx0.007518797;$
• the positive root of $R(t)$ is $\;t_h=\sqrt[\large3]{\dfrac{295+\sqrt{97798}}{81}} \approx1.957677294;$
• $\dfrac{\text dR}{\text dt}=\dfrac{1284t^2(133-162t^3)}{(133+81t^3)^3};$
• $\max R(t)=R_m=\dfrac{457}{32319}\approx0.014140289\;$ at $\;t_m=\sqrt[\large3]{\dfrac{133}{162}}\approx0.906083691;$
• $R(t)\;$ increases at $\;t\in[0,t_m];$
• $R(t)\;$ decreases at $\;t\in[t_m,t_h];$
• $R(t)\;$ is negative at $\;t\in(t_h,\infty).$

Finally, the inverse function is $$\rho(s,r)=\left(\dfrac{133}{81}\left(\dfrac{3}{2+s\sqrt{\dfrac{457-32319r}{214}}}-1\right)\right)^{\large\frac13},\tag{6.4}$$ where $\;s=\pm1.$

Accordingly, there are two branches of the inverse function $R^{-1}(r):$

• "plus"-branch $\;\rho(1,r),\quad r\in\left[\dfrac1{133},\dfrac{457}{32319}\right], \quad\rho(1,r)\in[0,t_m],\;$ and
• "minus"-branch $\;\rho(-1,r),\quad r\in\left[0,\dfrac{457}{32319}\right], \quad\rho(-1,r)\in[t_m,t_h].$

Easily to check, that

• $R(\rho(\pm1,r))=r,\quad r\in[0,\infty);$
• $\rho(1,R(t))=t,\quad t\in[0,t_m];$
• $\rho(-1,R(t))=t,\quad t\in[t_m,t_h].$

$\color{teal}{\textbf{6.3. Explicit expressions for superpositions.}}$

Since $$Q(t)\in(0,Q_m),\quad R(t)\in(0,R_m),\quad R_m=\dfrac{457}{32319}<Q_m,$$ then from $(5.1)$ should $$Q(t)\in\left(0,\dfrac{457}{32319}\right],\quad t\in\left((0,t_0]\cup[t_1,t_h]\right),\tag{6.5}$$ where $$\begin{cases} t_0=\theta\left(0,\dfrac{457}{32319}\right]\approx0.927295634,\\[4pt] t_m=\sqrt[\large3]{\dfrac{133}{162}}\approx0.936365798,\\[4pt] t_1=\theta\left(1,\dfrac{457}{32319}\right]\approx0.945494916,\\[4pt] t_h=\rho(-1,0)\approx1.957677294. \end{cases}\tag{6.6}$$

From $\;(5.1)\;R(u)=Q(w)\;$ should $\;u=\rho(s,Q(w))=g(s,w),\;$ where

$$g(s,t)=\left(\dfrac{133}{81}\;\left(\dfrac{3}{2+s\sqrt{\dfrac{457}{214}-\dfrac{96957t^2}{(133+81t^3)^2}}}-1\right)\right)^{\large\frac13},\quad s=-1,1.\tag{6.7}$$ Also, from $\;(5.1)\;R(v)=Q(u)\;$ should $v=g(s,u).$

On the other hand, from $\;(5.1)\;R(u)=Q(w)\;$ should $w=\theta(k,R(u))=h(k,u),\;$ where $$h(k,t)=\sqrt[\large4]{\dfrac{3424}{19683R(t)}} \sin\left(\dfrac13\left(2\pi k+\arcsin\left(4788\left(\dfrac{3R(t)}{3424}\right)^{\large\frac34}\right)\right)\right),\quad k=0,1.\tag{6.8}$$ Also, from $\;(5.1)\;R(v)=Q(u)\;$ should $u=h(k,v).$

At the same time, in accordance with $(5.1)$ should $$ug(s,u)h(k,u)=1.\tag{6.9}$$

$\color{brown}{\textbf{7. Proof, case A.}}$

In accordance with $(4.1),\quad u,v\in(0,1],\quad w\in[1,t_h],\quad $ and then should $$\;R(u)\in\left(\dfrac1{133},\dfrac{457}{32319}\right],\tag{7.1}$$ $$u w>1.\tag{7.2}$$

$\color{teal}{\textbf{7.1. Case A,$\;u\in[0,t_0].$}}$

Taking in account $(1.3),(7.1),(7.2),$ easily to get $h(0,u)<1,$ so $$\begin{align} &w=h(1,u)=\sqrt[\large4]{\dfrac{3424(133+81u^3)^2}{19683(133+590u^3-81u^6)}}\\[4pt] &\times\sin\left(\dfrac13\left(\pi-\arcsin\left(4788\left(\dfrac{3}{3424}\dfrac{133+590u^3-81u^6}{(133+81u^3)^2}\right)^{\large\frac34}\right)\right)\right), \end{align}\tag{7.3}$$ wherein $\;h(1,u)\;$ is decreasing function,

Let $H(t)=\dfrac1{h(1,t)},$ then

• for $\;u\in[0, H(0)]\quad u h(1,u) \le 1,\qquad H(0)\approx 0.621782171,$
• for $\;u\in[H(0), H(H(0))]\quad u h(1,u) \le 1,\qquad H(H(0))\approx 0.789031022,$
• for $\;u\in[H(H(0)),H(H(H(0))))]\quad u h(1,u) \le 1,\qquad H(H(H(0)))\approx 0.920622140,$
• for $\;u\in[H(H(H(0))),t_0]\quad u h(1,u) \le 1,\qquad t_0\approx 0.927295634.$

Therefore, $\text{for}\,u\in[0,t_0]\quad uh(1,u)\le1,$ and this contradicts with $(7.2).$

The plot of $\;uh(1,u)\;$ is shown below.

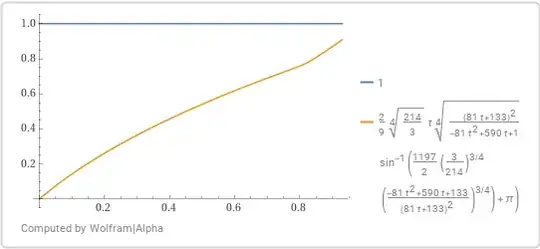
$\color{teal}{\textbf{7.2. Case A,$\;u\in(t_0,t_1).$}}$

In accordance with $(6.6),$ $$Q(t_0)=Q(t_1)=\dfrac{457}{32319}\approx0.014149289,\quad Q(t_m)=\dfrac{428}{3591}\sqrt[\large3]{\dfrac{2}{1197}}\approx0.014142960.$$ If $\;t\in(t_0,t_1),\;$ then $\;Q(t)\in\left(\dfrac{457}{32319},\dfrac{428}{3591}\sqrt[\large3]{\dfrac{2}{1197}}\right)\approx(0.014140289, 0.014142960).$

On the other hand, $$R(t)\le R_m=\dfrac{457}{32319}\approx0.014140289.$$ Therefore, the equation $$Q(u)=R(v)$$ has not real solutions in the described interval.

$\color{teal}{\textbf{7.3. Case A,$\;u\in[t_1,1].$}}$

Since $\;R(u)\in\left(\dfrac1{133}, \dfrac{457}{32319}\right)\equiv\left(\dfrac{243}{32319},\dfrac{457}{32319}\right),\;$ then

$\;w_0=h(0,u)\in[0.860147050,0.917509715],\; w_0<1,\;$ in contradiction with the conditions $(4.1).$

$\;(w_1=h(1,u)\in[0.943496443,1])\wedge(w_1\in[1,\infty)),$

$\mathbf{\{u,v,w\}=\{1,1,1\},\quad R(w)=Q(v)},\;$ and this corresponds with the inequality $(5.2).$

Therefore, the inequality $(2.1)\;\color{green}{\textbf{is proven in the case A}}.$

$\color{brown}{\textbf{8. Proof, case B,$\;u\in[1,t_h]$.}}$

$\color{teal}{\textbf{8.1. Preliminary notes.}}$

Taking in account $(4.3),$ should $\;u\in(1,t_h),\quad v\in(1,\infty),\quad w\in(0,1),\quad t_h=\rho(-1,0).$

Then $$\color{teal}{\mathbf{v=g(-1,u),\quad w=h(0,u)}}.\tag{8.1}$$

Graphic analysis of the functions $\;h(0,u)\;$ (orange line) and $\;u g(-1,u)\;$ (green line)

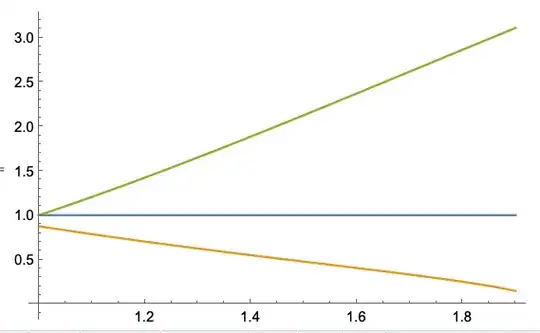
show, that both of them allow accurate linear approximations at the interval $\;u\in(1, t_h):$ $$h(0,u)\approx 0.8755-0.795(u-1)\pm 0.0135,\quad ug(-1,u)\approx 1+2.296(u-1)\pm 0.039.$$

So their product can be accurately approximated via quadratic function.

Therefore, the function $B(u)= u g(-1,u) h(0,u)$ is unimodal one in the interval $u\in(1,t_h).$

$\color{teal}{\textbf{8.2. Proof.}}$

From $(8.1),(6.7),(6.8)$ should that $$B(u)=ug(-1,u)h(0,u)=1\tag{8.2}$$ in the stationary points of the $f(u,v).$

Since $B(u)$ has the single maximum at $u\in(1,t_h),$ then equation $(8.2)$ can not have more than two roots in this interval.

Let us calculate the table $$\hspace{-32mu}\begin{vmatrix} u &\! v=g(-1,u) &\! w=h(0,u) & uvw & R(w) & Q(v)\\ 1.19 & \!1.177155295 &\! 0.711272982 &\! 0.996361720 &\! 0.012734730 &\! 0.012353493\\ 1.20 & \!1.185845698 &\! 0.703171746 &\! 1.000623827 &\! 0.012641505 & \!0.012221669\\ {\small 1.535129}&\!1.440476091 &\! 0.452219322 &\! 1.000000101 &\! 0.009467695 &\! 0.009467650\\ {\small1.535130}&\!1.440476742 &\! 0.452218605 &\! 0.999999621 &\! 0.009467687 &\! 0.009467642 \end{vmatrix}\tag{8.3}$$

Easily to see that there are two solutions of $(8.2)$,which are situated at the intervals $(1.19,1.20)$ and $(1.535129,1.535130)$ accordingly. At the same time, the functions $R(w)$ and $Q(v)$ are monotonic in these intervals. In particular, in the interval $(1.19,1.20)\quad R(w)>0.01264\;$ and $\;Q(v)<0.01236.$ This means that the inequality $(7.2)$ is satisfied at the interval $\;u\in(1.19,1.20),$ including the stationary point.

Similarly, at the interval $(1.535129,1.535130)$ easily to get $\;R(w)>0.009467686>0.009467651>Q(w).$ This means that the inequality $(7.2)$ is satisfied at the interval $\;u\in(1.535129,1.535130),$ including the stationary point.

Plot of the equality $uvw=1$ see below.

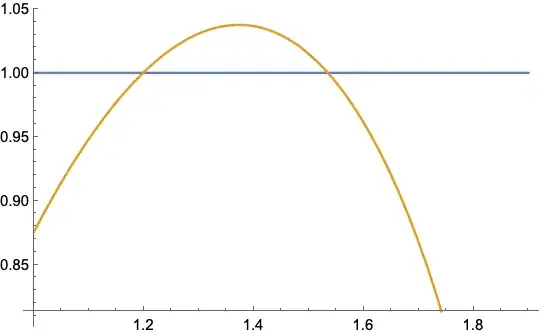
Therefore, the inequality $(4.5)$ $\color{green}{\textbf{is satisfied in the case B}}.$

$\color{green}{\textbf{Proved!!!}}$

Answer 4

Hard case $x\leq y\leq z$ and $\frac{y}{x},\frac{z}{y}\in[\frac{121}{84},\infty)$:

---

We have the function :

$$h\left(x\right)=\frac{13}{8+5x^{3}}+\frac{83}{1000}\left(1-\frac{2x}{2x+1}\right)+\frac{0.2375x}{x+1}$$

And :

$$g\left(x\right)=\frac{214}{133+81x^{3}}$$

Lemma :

And for $x\in[\frac{121}{84},\infty)$ a real number :

$$f''(x)=g''(x)-h''(x)>0$$

The problem :

The inequality is equivalent to :

$$\frac{x}{x+y}g\left(\frac{y}{x}\right)+\frac{y}{x+y}g\left(\frac{z}{y}\right)+\frac{1}{x+y}\frac{214z^{4}}{133z^{3}+81x^{3}}-\frac{\left(x+y+z\right)}{x+y}\geq 0$$

Now we use the lemma and Jensen's inequality we got ($f(x)=g(x)-h(x)$):

$$\frac{x}{x+y}f\left(\frac{y}{x}\right)+\frac{y}{x+y}f\left(\frac{z}{y}\right)+\frac{1}{x+y}\frac{214z^{4}}{133z^{3}+81x^{3}}-\frac{\left(x+y+z\right)}{x+y}\geq f\left(\frac{\left(z+y\right)}{x+y}\right)+\frac{1}{x+y}\frac{214z^{4}}{133z^{3}+81x^{3}}-\frac{\left(x+y+z\right)}{x+y}$$

Or after summation:

$$a(x,y,z)=\frac{x}{x+y}h\left(\frac{y}{x}\right)+\frac{y}{x+y}h\left(\frac{z}{y}\right)+\frac{1}{x+y}\frac{214z^{4}}{133z^{3}+81x^{3}}+g\left(\frac{\left(z+y\right)}{x+y}\right)-h\left(\frac{\left(z+y\right)}{x+y}\right)-\frac{\left(x+y+z\right)}{x+y}\geq 0$$

Remains to show that it is positive and BW helps but it's lenghty and I cannot check all the coefficients .

We have as expression expanded $y\geq 1$ a real number:

$$a(1,1+x,1+xy)= \mbox{the very long expression is given in the link blow}$$https://sagecell.sagemath.org/?q=ssnesu

Edit 18/04/2022:

Let $x\ge1 $ then it seems we have :

$$g''\left(x\right)-h''\left(x\right)-\frac{17}{100}f''\left(x\right)>0$$

Where :

$$f\left(x\right)=\frac{214x^{-1}}{133+81x^{3}}+\frac{x^{2}}{x}\frac{214}{133+81x^{-3}}-\frac{13x^{-1}}{8+5x^{3}}-\frac{x^{2}}{x}\frac{13}{8+5x^{-3}}$$

And :

$$h\left(x\right)=\frac{13}{8+5x^{3}}+\frac{0.13x}{x+1}+\frac{17}{100}f\left(x\right)$$

And :

$$g\left(x\right)=\frac{214}{133+81x^{3}}$$

So starting from :

$$b(x,y,z)=\frac{x}{x+y}K\left(\frac{y}{x}\right)+\frac{y}{x+y}K\left(\frac{z}{y}\right)+\frac{1}{x+y}\frac{214z^{4}}{133z^{3}+81x^{3}}+g\left(\frac{\left(z+y\right)}{x+y}\right)-K\left(\frac{\left(z+y\right)}{x+y}\right)-\frac{\left(x+y+z\right)}{x+y}\geq 0$$

Where :

$$K(x)=h(x)+0.17f(x)$$

We can use Buffalo's way but it's not for the hand .

Edit :

Using tangent line method on $r(\frac{\left(z+y\right)}{x+y})=g\left(\frac{\left(z+y\right)}{x+y}\right)-h\left(\frac{\left(z+y\right)}{x+y}\right)$,$q(x)=-0.027126(x-((((121)/(84))+1)/(((43)/(66))+1)))-((15865219)/(100000000))<r\left(x\right)$ , $a=(121/84+1)/(43/66+1)$ we have for $\frac{\left(z+y\right)}{x+y}\geq a$ :

$$a(x,y,z)=\frac{x}{x+y}h\left(\frac{y}{x}\right)+\frac{y}{x+y}h\left(\frac{z}{y}\right)+\frac{1}{x+y}\frac{214z^{4}}{133z^{3}+81x^{3}}+q\left(\frac{\left(z+y\right)}{x+y}\right)-\frac{\left(x+y+z\right)}{x+y}$$

$$a(1,1+x/2,1+((x y)/(y+1)))=\mbox{the very long expression is given in the link below}$$https://sagecell.sagemath.org/?q=gprkws

Answer 5

My first partial answer :

We introduce the function :

$$f\left(x\right)=\frac{1}{133+81x^{6}}$$

The function is convex for $x\in[1.03,\infty)$ so we have using Jensen's inequality :

$$g\left(x,y,z\right)=\left(x^{2}+0.001\right)f\left(\frac{\left(0.001\frac{z}{y}+xy\right)}{x^{2}+0.001}\right)+0.999f\left(\frac{z}{y}\right)+\frac{z^{8}}{133z^{6}+81x^{6}}-\frac{\left(x^{2}+y^{2}+z^{2}\right)}{214}\geq^?0$$

Using Buffalo's way we have :

$$g(x,1,(1+x^2)(1+y))= \mbox{the very very long expression is given in the link below} \ge 0$$https://sagecell.sagemath.org/?q=gmrshy

Where I only set the numerator For $x\in[0,1]$ and $y\ge0$