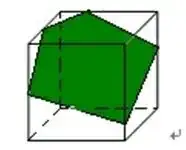
Came across this question in a children's recreational mathematics book. Apparently, the cross section of a cube cannot be a regular pentagon. It could be a irregular pentagon though.
But if we generalize this problem, can the cross section of parallelepiped be a regular pentagon? How do we prove that?