Convergent Improper integral whose integrand tends to a non zero finite limit as x tends to infinity.

Question

Let $f:\mathbb{R} \to \mathbb{R}$ be a continuous function such that $\int\limits_0^\infty f(x)dx$ exists. If $f(x)\ge 0 \,\forall x\, \in \mathbb{R}$, then prove or disprove that $\lim\limits_{x\to \infty}f(x)$ exists and is zero. If $f(x)$ is any function,then taking $f(x)=\sin(x^2),$ I am able to conclude that the result is false because $\lim\limits_{x\to \infty}\sin(x^2)$ does not exist even though $\int\limits_0^\infty \sin(x^2)dx$  is convergent. But in the case of non negative functions,I am neither able to prove the result nor do I get a counter example.Thank you in advance for your help.

Answer 1

Define a function $ f $ as the following graph shows :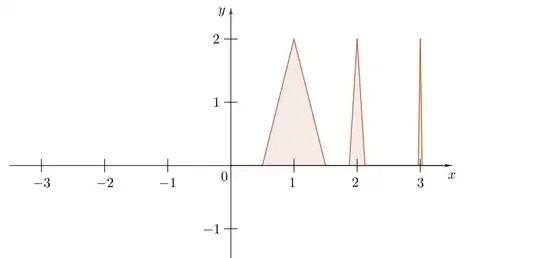

It is possible to define $ f $ explicitly, but that's not a big deal.

Its graph is formed of triangles centered at integers, each one centered at $ n\in\mathbb{N} $, has a base $ B_{n}=\frac{1}{n^{2}} $, and an altitude $ h=2 $, which means has an area $ \mathcal{A}_{n}=\frac{B_{n}\times h}{2}=\frac{1}{n^{2}} \cdot $

Then $$ \int_{0}^{+\infty}{f\left(x\right)\mathrm{d}x}=\sum_{n=1}^{+\infty}{\mathcal{A}_{n}}=\sum_{n=1}^{+\infty}{\frac{1}{n^{2}}}=\frac{\pi^{2}}{6} $$

$ \int_{0}^{+\infty}{f\left(x\right)\mathrm{d}x} $ converges, $ f\geq 0 $, but $ \lim\limits_{x\to +\infty}{f\left(x\right)}\neq 0 $ since $ \left(\forall n\in\mathbb{N}^{*}\right),\ f\left(n\right)=2 \cdot $

Answer 2

This is false. Here's a counterexample:

Pick a sequence $r_n$ of positive numbers with $r_n<1/2$ and $r_n\to 0$ when $n\to \infty$.

Given $n\in\mathbb{N}$, we define $f$ on the interval $[n,n+1]$ as follows:

• On $[n,n+1/2-r_n]$, $f$ is identically $0$.

• On $[n+1/2-r_n,n+1/2]$, the graph of $f$ is a straight line, with $f(n+1/2)=n$.

• On $[n+1/2,n+1/2+r_n]$, the graph of $f$ is a straight line, with $f(n+1/2+r_n)=0$.

• On $[n+1/2+r_n,n+1]$, $f$ is identically $0$.

Then the graph of $f$ on $[n,n+1]$ is a triangle of base $2r_n$ and height $n$, so that $$ \int_n^{n+1}f(x)dx=r_nn $$ Picking $r_n$ so that $\sum_n r_nn<\infty$, we obtain a counterexample, which is even unbounded!

---

The above method can be refined to obtain a continuous and non-negative function $f$ such that $\int_0^\infty f(x)dx<\infty$ and, for every rational number $q$, there is some sequence $x_n\to \infty$ with $f(x_n)\to q$. Since the rationals are dense, this means that for every real $y$ there is some $x_n\to \infty$ with $f(x_n)\to y$.

---

The above example has the property that the limit of $f(x)$ as $x\to \infty$ does not exist. This is no coincidence. If we replace "continuous" by $\lim_{x\to \infty} f(x)$ exists, then we can indeed infer that $\lim_{x\to \infty} f(x)=0$.

Answer 3

It is well known that $$\int\limits_0^\pi(\sin x)^n\,dx={\rm O}(n^{-1/2}) $$ (see here) The function $f(x)=|\sin x|^{x^4}$ does not tend to $0$ at infinity as $f((n+{1\over 2})\pi)=1.$ For $n\pi<x\le (n+1)\pi$ we have $$\int\limits_{n\pi}^{(n+1)\pi}|\sin x|^{x^4}\,dx \le \int\limits_{n\pi}^{(n+1)\pi}|\sin x|^{n^4}\,dx \\ = \int\limits_{0}^{\pi}(\sin x)^{n^4}\,dx= {\rm O}(n^{-2})$$ Therefore the integral is convergent.