2

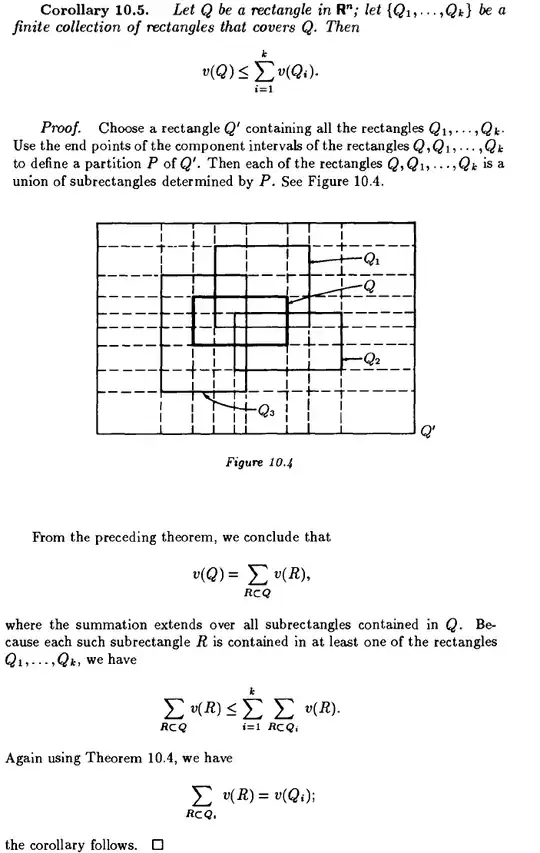
What shown below is a reference from "Analysis on manifolds" by James R. Munkres.

enter image description here

Well I don't formally understand why each $R\subseteq Q$ is contained in at least one of the rectangles $Q_1,...,Q_k$ so I ask to prove this formally. Could someone help me, please?

Antonio Maria Di Mauro
  • 5,226

2 Answers2

2

As stated in the beginning, "... each of the rectangles $Q,Q_1,\ldots, Q_k$ is a union of subrectangles determined by $P$".

Thus, $Q_j = \bigcup_{l=1}^{m_j} R_{jl}$ for each $j=1,\ldots,k$ and since $Q_1,\ldots, Q_k$ cover $Q$, we have

$$Q \subset \bigcup_{j=1}^k Q_j = \bigcup_{j=1}^k\bigcup_{l=1}^{m_j}R_{jl}$$

If $R \subset Q$, then as a member of the partition $P$ it must belong to the set $\{R_{jl}\}$ and so is contained in at least one of the rectangles $Q_1, \ldots , Q_k$.

RRL
  • 92,835
  • 7
  • 70
  • 142
  • why if $R\subset Q$ then as a member of the partition $P$ it must belong to the set ${R_{j,l}}$? – Antonio Maria Di Mauro May 19 '20 at 16:57
  • The partition contains rectangles that form the $Q_1,\ldots, Q_k$ and the remainder are not contained in any $Q_1,\ldots, Q_k$ -- although they may share a common face. If $R \subset Q$ then it can't belong to the second class can it? – RRL May 19 '20 at 17:02
  • Perhaps I begin to understand what you intend to say but unfortunately there is yet something that is obscure to me. So could you explain better, please? Forgive my confusion but I am an autodidact: unfortunately the professors of the university that I attend are not absolutely helpful for explanations and additionally the don't explain very well so I am forced to study by myself. – Antonio Maria Di Mauro May 19 '20 at 19:19
  • @RLL Perhaps I understood. For starters I observed that if $P$ is a partition of some rectangle $Q$ then for any subrectangles $S, T\in P$ it follows that $\overset{°}S,\overset{°}T\neq\varnothing$ and $S\cap\overset{°}T\neq\varnothing$ if and only if $S=T$. So if $R\subseteq Q\subseteq \bigcup_{j=1}^k\bigcup_{l=1}^{m_j} R_{j,l}$ then for what we observed above it follows that $R=R_{j,l}$ for some $j=1,...,k$ and $l=1,...,m_j$, right? – Antonio Maria Di Mauro May 19 '20 at 22:18
  • @AntonioMariaDiMauro: That is correct. Since $R \subset \bigcup_{j=1}^k\bigcup_{l=1}^{m_j}R_{jl}$ we can't have $R \cap \overset{°}T \neq \emptyset$ where $T \not\in {R_{jl}}$. – RRL May 20 '20 at 01:32
  • Hi, could I ask your assistance here? – Antonio Maria Di Mauro May 25 '20 at 11:23
1

Let $a = (a_x, a_y)$ be any interior point of $R$ (say the center of $R$ for sake of concreteness), and let $Q_j$ be any rectangle of $\{Q_1, \ldots, Q_k\}$ that contains $a$. We will show that $Q_j$ contains $R$. Let $Q_j$ be defined by the equations $x=l$, $x=r$, $y=d$, and $y=u$. Suppose for contradiction that $b = (b_x, b_y)\in R$ is not in $Q_j$. Without loss of generality suppose that $b_x > a_x$, that is $b$ is to the right of $a$ (the cases $b_x < a_x$, $b_y > a_y$, and $b_y < a_y$ are similar). Then the right vertical edge of $Q_j$ must pass between $c$ and $d$, i.e. $a_x \leq r < b_x$. But this means that $R$ would not be a subrectangle of $P$ (since the line $x=r$ would further partition $R$).

Anand
  • 1,246