Can one Integral have different solutions based on the algorithm used to solve it?

Question

This is my first post here and I searched the internet for things like "can u substitution yield an invalid result when finding an antiderivative?" and "manual integration and maxima produce different results" but this didn't find any useful links, which is why I'm posting here.

Background

I have a rather simple expression of which I want to find the indefinite integral/antiderivative of:

$$\frac{1}{y - \frac{115}{3}}$$

For context, this is part of a problem, where I am asked to solve the following ODE without using a SolveODE command:

$$\frac{dy}{dt} = -\frac{3}{50} \; \left(y - \frac{115}{3} \right)$$

Looking at the solution provided with the problem, I see that integrating the expression described at the beginning of this question should result in the following:

$$ \ln \left( \left|x - \frac{115}{3}\right| \right) + C $$

However, when solving using GeoGebra CAS to calculate the Integral (my exact input was Integral(1 / (x - 115 / 3))), I get the following output:

$$\ln \left( \left|3 \; x - 115\right| \right) + C$$

Using external help

Because I think that the antiderivative included in the official solution does not equal the one calculated by the Integral command in GeoGebra, I went to Integral-Calculator.com (the link leads to my calculation on the website) to find out what I did wrong.

I typed in my expression (1 / (y - 115 / 3)) and told it to solve for $y$.

A surprising result

Integral-Calcularot.com found both of the solutions.
Its results section has two parts: One describing a "manual" solve (whatever that means) and one which displays the solution calculated by the Maxima software:

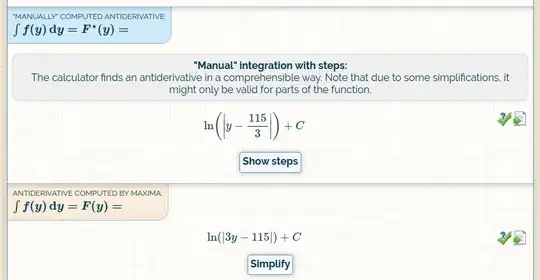
See screenshot

Several questions arise

How can there be two different (and conflicting) solutions to one math problem?
What did I miss?
Is one of the two solutions invalid?
Are the two solutions actually equal?

PS

AFTER typing my entire question, this website provided me with the following other (simular) question:

Different results when integrating 1/(x^2-9) with computer tools

I'm not sure if this would be considered a "duplicate" of the other one, but it doesn't help me understand my issue better; i.e. the two answers (or that question in and of itself) doesn't completely cover what I'm trying to do.

Thanks for reading!

Update

I've been testing and fiddling around a bit more and noticed the following:

It turns out flipping the fraction on its head and using $^{-1}$ leads to the desired behaviour. Any idea why?

Consider that C is an unspecified constant and that $ln(ab)=ln(a)+ln(b).$ — Paul, May 15 '20 at 14:46
The "solution" of an indefinite integral is a set, that is, the expression $f(x)+C$ for arbitrary constant represent a set of solutions. The solution can be represented in various ways but the resulting set solution must be the same — , May 15 '20 at 15:46
Does this answer your question? Getting different answers when integrating using different techniques — Sil, May 15 '20 at 18:14

Tanja · Accepted Answer · 2020-05-16T06:57:58.570

(this is my own answer)

My personal conclusion

Some questions are still open! (see below)

I tried around a bit more (see the "Update" section of my(=this) question), and it appears to be a quirk of GeoGebra.

Here is another example:

This behavior only occurs when the expressions are inserted directly into the Integral(...) command. If they are row-references (eg. Integral($1)), or defined constants (first, write A:=... and then in another line Integral(A)) this doesn't happen, and both will result in the expression calculated in line 4.

Confusing findings

This question is now closed, but only in a practical sense. As in: In practice, GeoGebra threats the inputs differently.

However, I still don't know if GeoGebra calculated correctly both times.

If we consider this as a bug in the software, which version is wrong (=which one is correct, and which result is caused by a buggy implementation)?

And remember: Integral-Calculator.com also provided two solutions for one input in a way similar to the example pictured above.

I posted this answer because it (at least in part) answers my question. This technically makes this answer wrong, but it's the least wrong answer available right now, so I want it to stay - at least until someone else provides a better one.

There are no unanswered questions. Your issue essentially amounts to the idea that $b$ and $b+1-1$, say, are different because they look different. — Paul, May 15 '20 at 21:20
@Paul I believe that $ln(|\pi x -42 |)+C$ does not equal $ln(|x - \frac{42}{\pi}|) +C$. — Tanja, May 16 '20 at 06:56
@Bernd-L: A way to avoid confusion about when $f(x)+C$ is equivalent to $g(x)+C$ is to see if $f(x)-g(x)$ is a constant. For $f(x)=\ln|\pi x-42|$ and $g(x)=\ln|x-42/\pi|$, we can write $$\begin{align}\ln|\pi x-42|-\ln|x-42/\pi|&=\ln\left(\pi\cdot|x-42/\pi|\right)-\ln|x-42/\pi|\ &=\ln\pi+\ln|x-42/\pi|-\ln|x-42/\pi|\ &=\ln\pi\quad\text{(const)}\end{align}$$ In the "$+C$" context, we have $g(x)+C=\ln\left|x-42/\pi\right|\color{red}{+C}$ and $f(x)+C=\ln|x-42/\pi|\color{red}{+\ln\pi+C}$; we allow the latter "$+C$" to absorb the $\ln\pi$, whereupon the two expressions are seen to be equivalent. — Blue, May 16 '20 at 07:28