1

What should be the graph of $$[y]=[\sin x]?$$(here $[a]$ reffers to the floor function.)

In my opinion if we just consider the square bounded by $(0,0) ,(0,1),(\pi,0)$ and $(\pi,1)$ then any point inside the square will satisfy the equation as $[y]=0$ and so is $[\sin x]$.

But as I looked up to desmos the graph shows something else.It just covers the border and not the points inside the square. Why is it so? I am unable to upload the screenshot of the graph here.

Calvin Khor
  • 36,192
  • 6
  • 47
  • 102
Neelarghya Kundu
  • 23

1 Answers1

5

I understand that you're looking for the set of pairs $$ \{ (x,y) \in \mathbb R^2: [y] = [\sin x] \}$$ Since this is not in the form $"y=f(x)"$, its not a graph, but a more general collection of points. In this specific case, you end up with filled in regions of the graph paper.

For $0\le x<\pi/2$, $\sin x\in [0,1)$ so $[\sin x]=0$. Then the set of points $y$ such that $[y] = 0$ is not a single point, but in fact a whole interval $[0,1)$.

The same is true for $\pi/2 < x \le \pi$, but at $x=\pi/2$, $[\sin \pi/2] = 1$, so then $y$ can take any value in $[1,2)$.

For the other half of the period, $\sin(x) \in [-1,0)$, and then $[\sin x] = -1$. In the end, you end up with a drawing something like:

     |        |
...[) (]    [) (]    ...
        (..)     (..)

Not sure what you put into Desmos, but here is how I coaxed Desmos into plotting the correct thing: 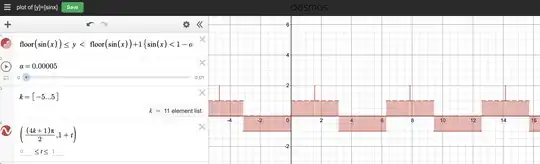enter image description here I had to manually add certain features of the graph that I wanted to emphasize, but if you zoom in then my graph becomes "wrong".

Calvin Khor
  • 36,192
  • 6
  • 47
  • 102
  • I understand that is not a function as for one value of x there can be many values of y.But the graph of desmos shows just the border.I did not understand the drawing you posted at last.Maybe because I recieved it in a jumbled up format. – Neelarghya Kundu May 15 '20 at 08:08
  • @NeelarghyaKundu I managed to force desmos to output what I wanted to see, but its a lot more complicated than just telling it $[y]=[\sin x]$ (see edit). Hopefully that justifies my ASCII art – Calvin Khor May 15 '20 at 08:10
  • Ok.Now I can see the result I wanted.I had simply typed floor(y)=floor (sin x).Can you give me an explanation why that is showing the wrong graph? – Neelarghya Kundu May 15 '20 at 08:14
  • And why do you think that your graph is wrong when enlarged and seen? – Neelarghya Kundu May 15 '20 at 08:17
  • Because I used a small parameter $\alpha$ to force desmos to not draw the region under the thin lines that stick out. If you zoom in around that line, you will see that actually, nothing at all is plotted to the left and right of the lines. But because of how fat a pixel is, the result looks OK at standard zoom. – Calvin Khor May 15 '20 at 08:20
  • Ok !Thanks a lot! – Neelarghya Kundu May 15 '20 at 08:24
  • @NeelarghyaKundu you're welcome :) – Calvin Khor May 15 '20 at 08:26