How do we find the number of sub-intervals whose intersection with the subset of the entire interval is non-empty?

Question

Suppose we have set $A=\left\{\frac{1}{k}:k\in\mathbb{N}\right\}$ and we divide interval $[0,1]$ into $n$ sub-intervals of equal length. How do we find the exact forumula (or approximation) of the number sub-intervals $f(n)$ whose intersection with $A$ is non-empty?

Here is what I found

$$\begin{array}{|c|c|} \hline n & f(n) \\ \hline 1 & 1 \\ \hline 2 & 2 \\ \hline 3 & 3 \\ \hline 4 & 4 \\ \hline 5 & 4 \\ \hline 6 & 5 \\ \hline 7 & 5 \\ \hline 8 & 6 \\ \hline 9 & 6 \\ \hline 11 & 6 \\ \hline 12 & 8 \\ \hline 13 & 7 \\ \hline 14 & 8 \\ \hline 15 & 8 \\ \hline \end{array}$$

It seems difficult to find an exact formula since $f(n)$ can, at times, go backwards as $n$ increases. An approximation is more reasonable.

In case you find an approximation, can you go into detail on how you found it?

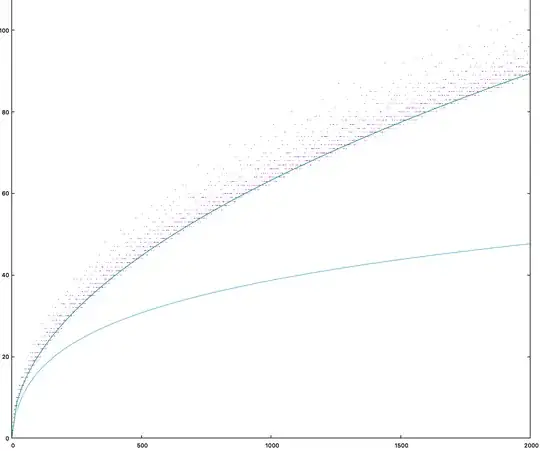
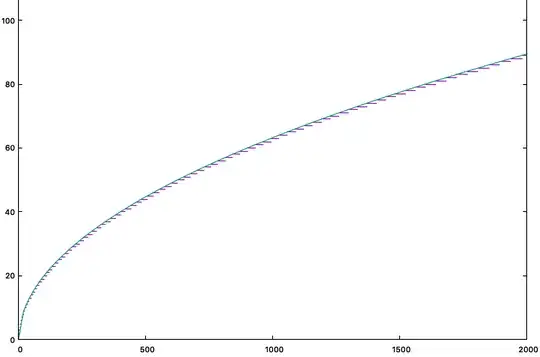
Edit: Using graphs I found the approximation is

$$f(n)\approx \frac{\ln(n)^2}{2\ln(2)^2}-\frac{3\ln(n)}{2\ln(2)}+4$$

When $n>32$ but I don't know how to mathematically derive it.

Edit: I was wrong, see @Joriki’s answer. However, he didn’t fully answer my second question.

How would you apply your process to approximate $f(n)$ for more complex sets such as

$$A=\left\{\frac{1}{2^x}+\frac{1}{2^y}+\frac{1}{2^z}:x,y,z\in\mathbb{N} \right\}\cap[0,1]$$

Answer 1

$A$ can be divided into two ranges: If the difference between adjacent values of $\frac1k$ is less than $\frac1n$, every interval is hit; whereas if the difference is greater than $\frac1n$, every interval is hit by at most $1$ element. As the difference between adjacent values of $\frac1k$ is roughly $\frac1{k^2}$, the transition between these two ranges is roughly at $k=\sqrt n$. Thus, each of the first $\sqrt n$ values of $k$ hits a new interval, and each of the remaining $\sqrt n$ intervals are hit by at least one value, so in total approximately $2\sqrt n$ intervals are hit.

Here’s a plot of the results up to 2000, compared to $2\sqrt n$ and also to your approximation, which seems to be wide of the mark (for instance, for $n=2000$ it yields about $48$, whereas the actual value is about $89$):

Here’s the code I used to generate the data for the plot.

The irregularity is entirely due to the fact that you’re counting the boundaries of the intervals towards both adjacent intervals. If you count the boundaries only towards the lower of the two intervals, so the intervals are $\left(\frac jn,\frac{j+1}n\right]$, the function becomes completely regular and is given by $\left\lfloor\sqrt{4n}\right\rfloor$, which you can derive by making the above consideration more rigorous and considering $\frac1k-\frac1{k+1}=\frac1{k(k+1)}=\frac1n$. Here’s a plot of this regular function (with and without the floor function applied):

Note that there are more points on the boundaries the more divisors $n$ has (in fact the count is incremented for each divisor of $n$ below $\sqrt n$, which is half the divisors of $n$, minus $\frac12$ if $n$ is a square). You can already see that in your data: $12$ is highly divisible and deviates upward, while $11$ and $13$ are primes and have no extra counts from the boundaries.