With three osculating circles, Descartes' formula relates the incircle's radius in terms of the circumcircle's and the three circle's radii or better their reciprocals, called curvatures: $$(\kappa_1 + \kappa_2 + \kappa_3 + \kappa_4)^2 = 2(\kappa_1^2 + \kappa_2^2 + \kappa_3^2 + \kappa_4^2) \tag{1}$$
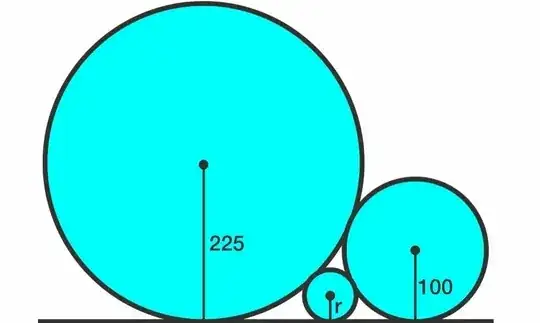
In a simplified variant where the circumcircle has curvature zero, i.e., degenerates into a common tangent the equation connecting the three circles, ignoring the incircle, simplifies into
$$\sqrt{\kappa} = \sqrt{\kappa_1} + \sqrt{\kappa_2} \tag{2}$$
This latter relation is usually derived by standard geometric methods. How can the technique of Circular Inversion Geometry be effectively employed to derive this result easily? Namely, how can one effectively choose the appropriate centre and radius of the inversive circle ?