Is there an intuitive proof of $\sin(x + y)= \sin x\cos y+ \sin y\cos x$ when $x + y > 90^\circ$?

Question

I saw nice geometric proof of $\sin{(x + y)} = \sin{x}\cos{y} + \sin{y}\cos{x}$ using unit circle. But I can't find proof when $x + y > 90^\circ.$

Is there intuitive, "simple" or geometric way to prove this? Can we maybe transform unit circle or what is going on here?

What have you tried? What fails in the prior proof when $x+y > 90^\circ$? — David G. Stork, May 01 '20 at 17:52
By reflection, we have $\sin(90^{\circ}+a)=\sin(90^{\circ}-a)$ and $\sin(180^{\circ}-a)=\sin(a)$. So you can always transform it back to the known case. — Integrand, May 01 '20 at 17:53
All identities outside of the first quadrant can be manipulated using either the related angle identities or the complementary angle identities. — Andrew Chin, May 01 '20 at 17:55
Because the stacking right triangles one on another is not possible for, say, $\sin {(100 ° + 120 °)}$. All proofs shows the situation for angles $x, y < 90^\circ$ (for example, $\sin{(30 ° + 45 °)}$. — 1b3b, May 01 '20 at 17:58
@Integrand, I feel that is good way but can you systematically prove it for me in not-brute-force way. I always find myself stucked. Thanks — 1b3b, May 01 '20 at 18:01
The addition formulas are true for general angles because of the Principle of the Analytic Continuation. A proof of the formulas which doesn't need the condition $x + y < 90$ is the one using Ptolemy's theorem about the cyclic quadrilaterals. You can check Trigonometry by I.M Gelfand, He proves the formulas using Ptolemy's theorem in the appendix to Chapter 6, and talks about the Principle a bit at the Beginning of Chapter 7. — dude076, May 01 '20 at 18:30
Related (duplicate?): "Looking for an alternative proof of the angle difference expansion". In particular, my answer shows how to adapt my Wikipedia-famous diagram from this answer to a couple of non-acute cases. — Blue, May 01 '20 at 23:46
@Blue, thanks but it seems to me that descripiton of aforementioned question requires only proofs from Euclidean geometry. I will certainly study your proof. — 1b3b, May 02 '20 at 10:43
@1b3b When I teach this to my students I start by proving the formula for $\cos(\alpha-\beta)$ (which can be done geometrically for arbitrary angles), and from that the formula for $\sin(\alpha+\beta)$ can be derived, using $\sin(\alpha+\beta)=\cos(\pi/2-\alpha-\beta)$. — Intelligenti pauca, May 02 '20 at 21:51
Several of the answers to How can I understand and prove the "sum and difference formulas" in trigonometry? cover cases where the sum of angles is greater than $90^\circ,$ including sums of angles of any size. — David K, Apr 17 '25 at 15:13

score 4 · Accepted Answer · answered May 01 '20 at 22:26

4

Let $x$ and $y$ be any argument angles in the Argand diagram. Then, $ e^{i (x+y)} = e^{i x } e^{i y }$, or

$$\cos (x+y)+ i\sin(x+y) =(\cos x+i \sin x)(\cos y+i \sin y)$$

Match the real and imaginary parts to obtain

$$\cos(x+y)=\cos x\cos y-\sin x\sin y$$ $$\sin(x+y)=\sin x\cos y+\cos x\sin y$$

answered May 01 '20 at 22:26

Quanto

120,125

The only thing that is perhaps a little confusing here is the direction of the implications. I think it is more natural to prove $e^{i(x + y)}$ (#) using this basic trig identities (sine and cosine of the sum of angles) than vice versa (but I know that $e^{i(x + y)}$) can be proved by definition $e^{i\theta} = (1 + \frac{i\theta}{n})^n$ setting $\theta = x + y,$ and then of course (#) holds). Thanks for the nice trick, I didn't think of that! – 1b3b May 01 '20 at 22:39

score 3 · Answer 2 · answered Aug 06 '21 at 21:57

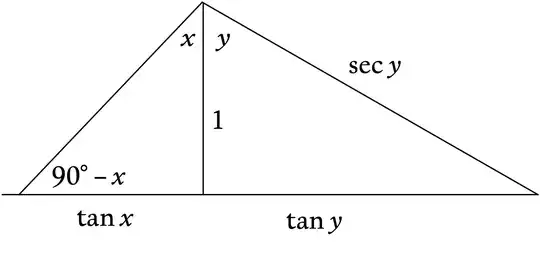
Sorry I didn’t see this one earlier. When sitting in on high-school trigonometry classes, I’ve wondered about what the various proofs of sine addition might be, and which one might be the best. There is the purely geometric proof, which you know, but is no good for $x+y>90^\circ$. And there is the proof recommended by @intelligentipauca, involving a minimum of geometry but a great load of algebraic manipulation, and which ends up with no intuition on the student’s part. Here’s a proof that’s in between, involving a minimum of geometry, of trigonometry, and of algebra. It’s only good for $x<90^\circ$, similarly for $y$, but $x+y$ can be anything smaller than $180^\circ$.

Start with a horizontal line, and erect a perpendicular segment on it, and call its length $1$. Draw angles $x$ and $y$ sharing the perpendicular, but on opposite sides, so that they make an angle of $x+y$ together.

Now you see that the two horizontal segments are $\tan x$ and $\tan y$, and that the right-hand hypotenuse is $\sec y$.

Next, call in the Law of Sines, according to which \begin{align} \frac{\sin(x+y)}{\tan x + \tan y}&=\frac{\sin(90^\circ-x)}{\sec y}\\ &=\cos x\cos y\,. \end{align} Now multiply both sides by $\tan x+\tan y$ and get $\sin(x+y)=(\tan x+\tan y)\cos x\cos y$. And there’s your addition formula for sines.

score 0 · Answer 3 · answered Apr 16 '25 at 16:00

The way I was introduced to the identities in high school precal. Let's start with subtraction of angles.

Let $A = (\cos\alpha, \sin\alpha)$ and $B = (\cos\beta, \sin\beta)$ be two points on the unit circle.

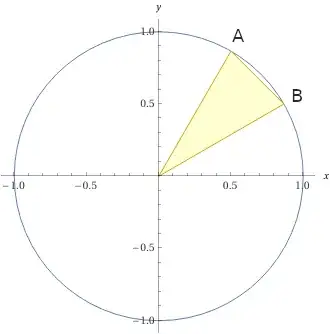
Then the distance between them is

$$d = \sqrt{(\cos\alpha - \cos\beta)^2 + (\sin\alpha - \sin\beta)^2}$$ $$= \sqrt{\cos^2\alpha - 2\cos\alpha\cos\beta + \cos^2\beta + \sin^2\alpha - 2\sin\alpha\sin\beta + \sin^2\beta}$$ $$= \sqrt{(\cos^2\alpha + \sin^2\alpha) + (\cos^2\beta + \sin^2\beta) - 2\cos\alpha\cos\beta - 2\sin\alpha\sin\beta}$$ $$= \sqrt{2 - 2\cos\alpha\cos\beta - 2\sin\alpha\sin\beta}$$

Now, let's rotate the coordinate system so that $B = (1, 0)$ and $A = (\cos(\alpha - \beta), \sin(\alpha - \beta))$.

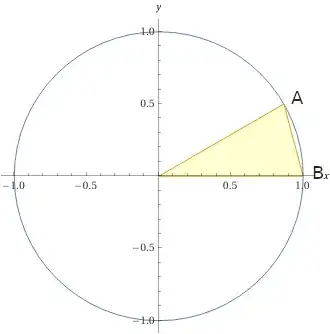
Then the distance between the points is:

$$d = \sqrt{(\cos(\alpha - \beta) - 1)^2 + \sin^2(\alpha-\beta)}$$ $$= \sqrt{\cos^2(\alpha - \beta) - 2\cos(\alpha - \beta) + 1 + \sin^2(\alpha-\beta)}$$ $$= \sqrt{1 + (\cos^2(\alpha - \beta) + \sin^2(\alpha-\beta)) - 2\cos(\alpha - \beta)}$$ $$= \sqrt{2 - 2\cos(\alpha - \beta)}$$

But since the distance between $A$ and $B$ must be the same either way, we have:

$$= \sqrt{2 - 2\cos(\alpha - \beta)} = \sqrt{2 - 2\cos\alpha\cos\beta - 2\sin\alpha\sin\beta}$$ $$= 2 - 2\cos(\alpha - \beta) = 2 - 2\cos\alpha\cos\beta - 2\sin\alpha\sin\beta$$ $$-2\cos(\alpha - \beta) = -2\cos\alpha\cos\beta - 2\sin\alpha\sin\beta$$ $$\boxed{\cos(\alpha - \beta) = \cos\alpha\cos\beta + \sin\alpha\sin\beta}$$

Now, let's do $\cos(\alpha + \beta)$. That's equivalent to $\cos(\alpha - (-\beta))$, so by the above formula,

$$\cos(\alpha + \beta) = \cos\alpha\cos(-\beta) + \sin\alpha\sin(-\beta)$$

But $\cos$ is even (i.e., $\cos(-\beta) = \cos(\beta)$) and $\sin$ is odd (i.e., $\sin(-\beta) = -\sin(\beta)$), so:

$$\boxed{\cos(\alpha + \beta) = \cos\alpha\cos\beta - \sin\alpha\sin\beta}$$

Now we need similar formulas for $\sin$. Start by using the Pythagorean identity

$$\sin^2(\alpha - \beta) + \cos^2(\alpha - \beta) = 1$$ $$\sin^2(\alpha - \beta) + (\cos\alpha\cos\beta + \sin\alpha\sin\beta)^2 = 1$$ $$\sin^2(\alpha - \beta) + \cos^2\alpha\cos^2\beta + 2\cos\alpha\cos\beta\sin\alpha\sin\beta + \sin^2\alpha\sin^2\beta = 1$$ $$\sin^2(\alpha - \beta) + (1 - \sin^2\alpha)(1 - \sin^2\beta) + 2\cos\alpha\cos\beta\sin\alpha\sin\beta + \sin^2\alpha\sin^2\beta = 1$$ $$\sin^2(\alpha - \beta) + 1 - \sin^2\alpha - \sin^2\beta + \sin^2\alpha\sin^2\beta + 2\cos\alpha\cos\beta\sin\alpha\sin\beta + \sin^2\alpha\sin^2\beta = 1$$ $$\sin^2(\alpha - \beta) = \sin^2\alpha + \sin^2\beta - 2\sin^2\alpha\sin^2\beta - 2\cos\alpha\cos\beta\sin\alpha\sin\beta$$ $$\sin^2(\alpha - \beta) = (\sin^2\alpha)(1 - \sin^2\beta) + (\sin^2\beta)(1 - \sin^2\alpha) - 2\cos\alpha\cos\beta\sin\alpha\sin\beta$$ $$\sin^2(\alpha - \beta) = \sin^2\alpha\cos^2\beta + \cos^2\alpha\sin^2\beta - 2\cos\alpha\cos\beta\sin\alpha\sin\beta$$ $$\sin^2(\alpha - \beta) = (\sin\alpha\cos\beta - \cos\alpha\sin\beta)^2$$ $$\sin(\alpha - \beta) = \pm (\sin\alpha\cos\beta - \cos\alpha\sin\beta)$$

Which leaves the question: Plus or minus? If we plug in $\beta = 0$, we get:

$$\sin(\alpha) = \pm (\sin\alpha\cos(0) - \cos\alpha\sin(0)) = \pm \sin\alpha$$

Similarly, if $\alpha = 90°$, then:

$$\sin(90° - \beta) = \pm (\sin(90°)\cos\beta - \cos(90°)\sin\beta)$$ $$\cos(\beta) = \pm \cos\beta$$

Clearly, plus is the correct choice.

$$\boxed{\sin(\alpha - \beta) = \sin\alpha\cos\beta - \cos\alpha\sin\beta}$$

And, using the same odd/even function approach as before,

$$\sin(\alpha + \beta) = \sin\alpha\cos(-\beta) - \cos\alpha\sin(-\beta)$$ $$\boxed{\sin(\alpha + \beta) = \sin\alpha\cos\beta + \cos\alpha\sin\beta}$$

Note that I have not made an acute angle assumption anywhere.

Is there an intuitive proof of $\sin(x + y)= \sin x\cos y+ \sin y\cos x$ when $x + y > 90^\circ$?

3 Answers3