What shown below is a reference from "Analysis on manifolds" by James R. Munkres
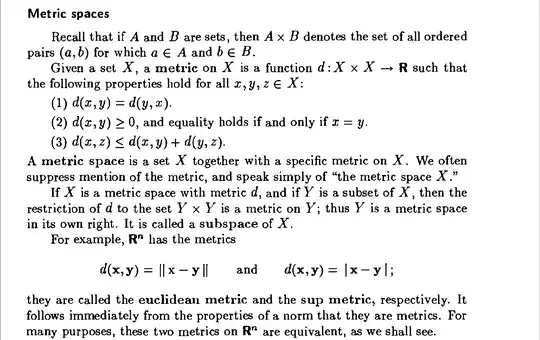
I don't know which is sup metric. Show the definition and show that the Euclidean metric is equivalent to sup metric.
Could someone help me, please?
What shown below is a reference from "Analysis on manifolds" by James R. Munkres
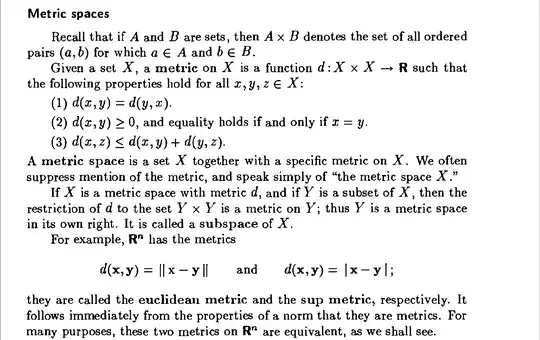
I don't know which is sup metric. Show the definition and show that the Euclidean metric is equivalent to sup metric.
Could someone help me, please?
The Euclidean metric is given by $d(\mathbf{x}, \mathbf{y})=\sqrt{\sum_{i=1}^n (x_i-y_i)^2}$ while the sup metric is given by $d'(\mathbf{x}. \mathbf{y})= \max_{1 \le 1 \le n} |x_i -y_i|$.
They are equivalent because for all vectors
$$d'(\mathbf{x}. \mathbf{y}) \le d(\mathbf{x}. \mathbf{y}) \le \sqrt{n}d'(\mathbf{x}. \mathbf{y})$$
so being "near" in one metric means being "near" in the other, so they define the same open and closed sets, bounded sets, convergent sequences etc etc. Even uniform convergence in one is equivalent to uniform convergence in the other.
Euclidean norm and $\sup$-norm are defined on p. 4: $\lVert x \rVert = \sqrt{\langle x, x \rangle} = \sqrt{\sum_{i=1}^nx_i^2}$ and $\lvert x \rvert = \max(\lvert x_1 \rvert,\ldots,\lvert x_n \rvert)$. This induces the Euclidean metric $d(x,y) = \lVert x -y \rVert$ and the $\sup$-metric $d(x,y) = \lvert x -y \rvert$. Also on p.4 Munkres states that $\lvert x \rvert \le \lVert x \rVert \le \sqrt{n}\lvert x \rvert$. The proof is straightforward and implies that the metrics are equivalent:
$$\lvert x \rvert^2 = \max(\lvert x_1 \rvert^2,\ldots,\lvert x_n \rvert^2) = \max(x_1^2,\ldots,x_n^2) \le \sum_{i=1}^nx_i^2 \le n \max(x_1^2,\ldots,x_n^2) = n \lvert x \rvert^2 .$$