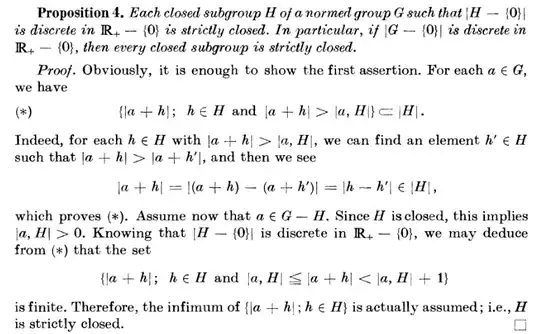0

I have a quiestion. I don't understand the meaning of "discrete" in the next theorem. I don't get why the author deduces that the set in the antepenultimate line is finite. The book is "Non-Archimedean Analysis" by S. Bosch, U. Güntzer and R. Remmert. The proposition is in page 15. Thank you for your help.

enter image description here

José Carlos Santos
  • 440,053
Juan Caldera
  • 1
  • Presumably, for $A\subseteq G$, the author indicates with $\lvert A\rvert$ the image set of $A$ via the norm function. –  Apr 25 '20 at 07:30
  • 1
    Every point has a neighborhood free of other points of the set. – Conifold Apr 25 '20 at 07:37
  • Yes, $|A|={|a|,:, a\in A}$. – Juan Caldera Apr 25 '20 at 14:39
  • I thinking in a set with this definition of discrete, but the set in antepenultimate line wouldn't be finite. For example, ${1/n,:, n\in \mathbb{N}}$ or any translation and / or dilatation of this set. – Juan Caldera Apr 25 '20 at 14:47
  • @JuanCaldera you are missing the hypothesis that $H$ is a subgroup of $G$ and not a simple subset. – Chilote May 03 '20 at 18:36

1 Answers1

1

Usually, in this context, discrete means that the subspace topology of $|H-\{0\}|$ as a subspace of $(0,\infty)$ equipped with the order topology is the discrete topology. In other words, a subset $A$ of $(0,\infty)$ is discrete if $A$ can be covered by disjoint open intervals each of them containing only one element of $A$.

Every subgroup of $((0,\infty),\cdot)$ is either dense or discrete. And if it is discrete and non-trivial, then it is cyclic, i.e. of the form $\{s^n:n\in\mathbb{Z}\}$ for some $s\neq1$, $s>0$. A proof of this fact can be found in B.5.2 of Niel Shell, Topological fields and near valuations, Monographs and textbooks in pure and applied mathematics, vol. 135, Dekker, 1990.

In your posted Proposition 4, we can assume that $|H-\{0\}|=\{s^n:n\in\mathbb{Z}\}$ for some $s\neq1$, $s>0$.

Therefore, if $\alpha>0$ then $|H-\{0\}|\cap [\alpha,\alpha+1)$ is finite. Then every subset of it will be finite as well, indeed, $\{|a+h|: h\in H \mbox{ and }|aH|\leq|a+h|<|aH|+1 \}$ is finite because it is a subset of $$|H-\{0\}|\cap [|aH|,|aH|+1).$$

Chilote
  • 4,367
  • 1
  • 26
  • 51