0

SEE AUTHOR'S ANSWER BELOW

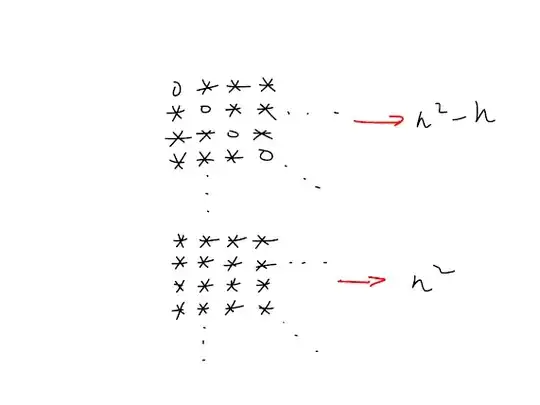
So I'm trying to derive the dimensions of both $Skew_{n\times n}(\mathbb{R})$ and $Sym_{n\times n}(\mathbb{R})$. I know that $\dim(M_{n\times n}(\mathbb{R}))=n^2$, but I need to see something else to start.

Diagrammatically, how can I reason these relations? As, for example, something like this:

image

Just as an aside, perhaps the modern-day, fast-paced nature of discovery is prohibiting us from seeing the utility of our axioms. What do you think?

YuiTo Cheng
  • 3,841
Trancot
  • 4,127
  • Sym. -> $M = M^t$ and Skew-Sym. -> $M=-M^t$, but which is bigger? – Trancot Apr 16 '13 at 23:59
  • Is there a simple proof as to why skew-symmetric matrices must have all zeros for their diagonal entries? – Trancot Apr 17 '13 at 00:03
  • Related (answered before): http://math.stackexchange.com/questions/185802/dimensions-of-symmetric-and-skew-symmetric-matrices – Lord Soth Apr 17 '13 at 00:04
  • 1
    Say $m$ is a diagonal entry of a real skew-symmetric $M$. Since $M = -M^t$, we have $m = -m \implies m = 0$. – Lord Soth Apr 17 '13 at 00:05
  • @LordSoth See my most recent edit... – Trancot Apr 17 '13 at 01:15
  • These symbol-form modes of reasoning are beginning to get on my nerves. I understand the ideas, it's just this naming policy in mathematics seems unnecessarily taxing. Diagrammatic representations seems more speaking... – Trancot Apr 17 '13 at 01:17
  • Diagrams or figures are helpful in understanding concepts, but they are sometimes misleading. That is why people usually prefer the uglier but safer way of "symbol-modes of reasoning." I do not understand what your diagrams represent here though. I guess in the first one, you attempt to conclude that the dimension of the skew symmetrics is $n^2-n$, which is not correct. Since the upper diagonals are precisely the negatives of the lower diagonals, you may also remove the upper diagonals (or the lower diagonals), and conclude that the dimension is $\frac{n^2-n}{2}$ (as shown in the link). – Lord Soth Apr 17 '13 at 01:27
  • 1
    Note, interestingly enough, that $M_n = Skew_n \oplus Sym_n$. – Alex Provost Apr 17 '13 at 01:35
  • @Silencer Oh, yes. I know that. Thank you! ^_^ – Trancot Apr 17 '13 at 01:46
  • @LordSoth No attempt to conclude. Only an attempt to "diagrammatically reason." See my answer below. What do you think? Any good? Would it suffice for an answer in a linear algebra class solution set? – Trancot Apr 17 '13 at 01:48
  • 1
    Whether or not this argument suffices would depend on your teacher. I personally accept proofs of this form, given that they display valid logic. I am not sure I agree with user Lord Soth in the opinion that people usually prefer uglier symbol porn over diagrammatic reasoning. I often - including in this case - find the pictorial method much more enlightening, efficient, elegant, and overall preferable (hence +1 for you). Note what you call "cardinality of matrix parameters" below in a comment falls under the more standard umbrella term "degrees of freedom." – anon Apr 17 '13 at 02:45
  • @anon Hey, anon, what's your background/story? – Trancot Apr 17 '13 at 02:55

1 Answers1

0

\begin{eqnarray} M_{n \times n}(\mathbb{R}) & \text{has form} & \begin{pmatrix} *&*&*&*&\cdots \\ *&*&*&*& \\ *&*&*&*& \\ *&*&*&*& \\ \vdots&&&&\ddots \end{pmatrix} \hspace{.5cm} \text{with $n^2$ elements}\\ \\ \\ Skew_{n \times n}(\mathbb{R}) & \text{has form} & \begin{pmatrix} 0&*'&*'&*'&\cdots \\ *&0&*'&*'& \\ *&*&0&*'& \\ *&*&*&0& \\ \vdots&&&&\ddots \end{pmatrix} \end{eqnarray} For this bottom formation the (*)s and (*')s are just operationally inverted forms of the same number, so the array here only takes $\frac{(n^2 - n)}{2}$ elements as an argument to describe it. This appears to be an array geometry question really... I suppose if what I'm saying is true, then I conclude that because $\dim(Skew_{n \times n}(\mathbb{R}) + Sym_{n \times n}(\mathbb{R})) = \dim(M_{n \times n}(\mathbb{R}))$ and $\dim(Skew_{n \times n}(\mathbb{R}))=\frac{n^2-n}{2}$ then we have that \begin{eqnarray} \frac{n^2-n}{2}+\dim(Sym_{n \times n}(\mathbb{R})))=n^2 \end{eqnarray} or \begin{eqnarray} \dim(Sym_{n \times n}(\mathbb{R})))=\frac{n^2+n}{2}. \end{eqnarray}

Trancot
  • 4,127
  • It also seems to touch on the topic of the cardinality of matrix parameters. – Trancot Apr 17 '13 at 02:01
  • 1
    Note that you can use diagrammatic reasoning in order to show that $\dim {\rm Sym}=\frac{n^2+n}{2}$ too (so using $M\cong {\rm Sym}\oplus{\rm Skew}$ can be avoided if one were so inclined). The idea is that the entries in the diagonals and (say) the lower triangle can all be varied freely while the upper triangle is always fully determined by the lower triangle. – anon Apr 17 '13 at 02:48