Good Stopping Criteria for Persistent Homology

Question

I've recently coded up a suite of algorithms for computing the persistent homology for various data sets (small data sets roughly around 30 data points). A question has come to my mind about how to find an optimal stopping criterion for generating the Vietoris-Rips sequence.

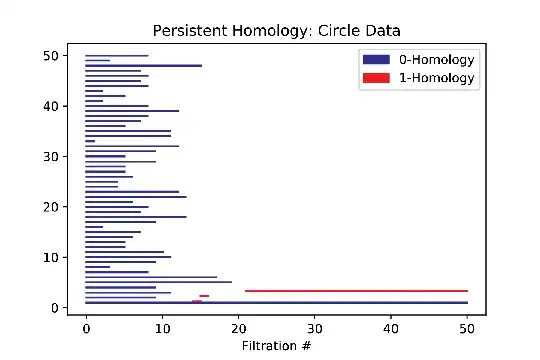
The Vietoris-Rips sequence is constructed by forming simplicial complexes of the data points by systematically increasing the threshold distance allowed to draw an edge between two points. Eventually, as the threshold distance increases, the image is filled with more and more simplexes until eventually the resulting space is a simply connected blob. For those unfamiliar with persistent homology, the desired result of the algorithm is to produce a graph called a bar code which is a visual representation of the homological features that are "born" at some stage of the Vietoris-Rips sequence, and eventually "die" when enough simplexes are drawn in the data. As an example, below are screen images of an initial data set (looking vaguely circular), a later shot after some simplexes have been filled in, and the resulting barcode.

My question is: what is a good stopping criterion for determining the largest distance needed in the Vietoris-Rips sequence to accurately capture all of the interesting (i.e. persistent) topological features of the data set? The problem with these algorithms is that they are extremely expensive, generating enormous matrices (for context, I relied almost exclusively on "A Roadmap for the Computation of Persistent Homology" by Otter et al. for my specific implementation). Two clear ideas for stopping criteria have come to mind:

1. Compute the Vietoris-Rips sequence up to some fraction of the maximal distance seen in the data set (essentially guesstimating, unless there are good lower bounds on when to expect topological features to die out).
2. Simply stopping when all ${N\choose 2}$ edges are drawn between the data points, most likely generating an unnecessarily long filtration and costing much time and computational energy to generate.

This is my first venture into topological data analysis. It would be great to know what literature there is published on cutting the computational complexity of these algorithms.

Answer 1

The question you ask is very relevant and difficult! I don't think we have great answers yet.

There are several positive results showing that if you have a nice space $M$ and a finite noisy sampling $X$ from $M$ that is dense enough, then you can recover the homology of $M$ from the persistent homology of $X$. See for example Theorem 3.6 of https://geometrica.saclay.inria.fr/team/Steve.Oudot/papers/co-tpbr-08/co-tpbr-08.pdf, or Figure 2.4 of http://www.paulbendich.com/pubs/analyz.pdf (the true homology of $M$ is given by the persistent homology points in the yellow rectangle in the left of this figure). These results in some sense tell you how large you need to let the scale parameter grow, but those bounds typically are in terms of the curvature of the unknown space $M$. (One could try to estimate the curvature or reach of a space from a finite sample, see for example https://projecteuclid.org/euclid.ejs/1555056153, though that is also not easy.) Furthermore, these results recovering the homology of $M$ typically require prohibitively restrictive assumptions on the sampling --- your sampling would have to have many more points than one typically has in practice.

In practice, I advise people to start by setting the maximum scale parameter to be quite small. Increase the maximum scale parameter and recompute persistent homology. As you redo these computations, you get to see more and more of the persistent homology barcodes. Keep increasing the maximum scale parameter towards the limits of what your machine can handle, and consider doing lengthier and more expensive computations (with larger maximum scale parameters) only if you are seeing features you find interesting. Of course, as you point out, the computational complexity may quite quickly exceed what your machine can handle.

There are some results, by my collaborators and me and others, that say that in some sense there's no limit on what scale parameters can lead to interesting topology. Let $S^1$ be the circle, equipped with the geodesic metric, and let the circumference of this circle be 1. So the diameter of this geodesic circle is $\frac{1}{2}$. (The same exact results below also hold for the circle with the Euclidean metric, just at different scale parameters.) For $0<r<\frac{1}{3}$, the Vietoris--Rips complex of this circle at scale $r$ is homotopy equivalent to the circle $S^1$. For $\frac{1}{3}<r<\frac{2}{5}$, the Vietoris--Rips complex of this circle at scale $r$ is homotopy equivalent to the 3-sphere $S^3$. For $\frac{2}{5}<r<\frac{3}{7}$, the Vietoris--Rips complex of this circle at scale $r$ is homotopy equivalent to $S^5$. More generally, for $\frac{k}{2k+1}<r<\frac{k+1}{2k+3}$, the Vietoris--Rips complex of this circle is homotopy equivalent to the $(2k+1)$-sphere $S^{2k+1}$. So we have a single persistent homology bar in homological dimension $2k+1$ with start time $\frac{k}{2k+1}$ and with death time $\frac{k+1}{2k+3}$. So the Vietoris--Rips complex is not contractible until we reach or exceed the diameter of the circle, i.e., until $r\ge \frac{1}{2}$. If you care about these higher-dimensional spheres, which give shorter and shorter persistent homology bars in higher and higher homological dimensions, then you can't stop your computation short before reaching the diameter ($r=\frac{1}{2}$) of the dataset. Here the dataset is the entire circle, but these same short higher-dimensional barcodes appear even if you have a (sufficiently dense) finite sample from the circle. But perhaps you don't care about these higher-dimensional spheres, in which case you can then safely end your computation at $r=1/3$ without cutting off any of the persistent homology bars you care the most about, which in this case is probably the single 1-dimensional persistent homology bar and nothing more.