1

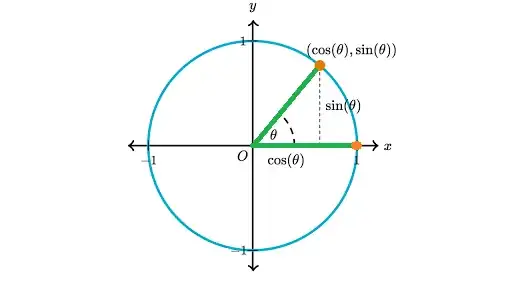
So I read online that to find angle $\theta$ between two vectors $v=(v_1,...,v_n)$ and $u=(u_1,...,u_n)$, we solve for $\cos(\theta)=\frac{u \text{ dot } v}{\|u\|\|v\|}$. But I don't understand why? why is this formula true?

I understand that the squared norm of a vector $u$ is $\sum_1^n u_i^2$ by the Pythagoras theorem. Would this help prove the result?

Jean Marie
  • 88,997
user 6663629
  • 234

1 Answers1

2

$$\frac u{\|u\|}, \frac v{\|v\|}$$ are unit vectors, and WLOG we can take the dot product of the two unit vectors $(1,0)$ and $(\cos\theta,\sin\theta)$, which form an angle of aperture $\alpha$:

$$(1,0)\cdot(\cos\alpha,\sin\theta)=1\cdot\cos\theta+0\cdot\sin\theta=\cos\theta.$$

As the dot product is invariant to a rotation, the dot product is always the cosine of the angle between the vectors.

enter image description here

  • When you define the dot product through coordinates, the crux of the issue is precisely why it is invariant by rotation. – Raoul Apr 13 '20 at 12:47
  • @Raoul: I know, but I didn't want to clutter the answer with the angle addition formula. –  Apr 13 '20 at 12:50
  • sorry sir, what if the vectors are in n dimensional instead of 2? how do you generalize? – user 6663629 Apr 13 '20 at 12:52
  • Using the same argument, these two vectors can be seen as $n$-dimensional and you can rotate them in $n$-space for generality. $(1,0,0,\cdots0)\cdot(\cos\theta,\sin\theta,0,\cdots0)$. –  Apr 13 '20 at 13:01