Solve for the angle UFO with the russian triangle

Question

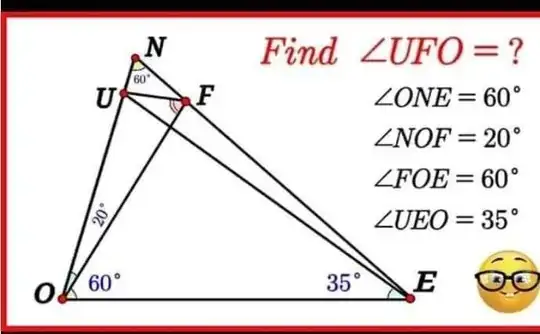
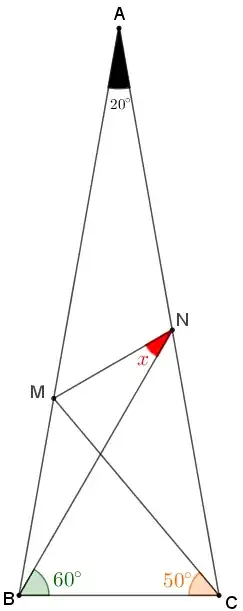
I know that this question has been posted already, but I saw that is possible to draw the triangle of the question inside of the russian triangle. Can someone help me to finish the question using this?

I find a lot of angles and I got the equation $∠UFO+∠UFN=100°$, but I couldn't find the value of $∠UFN$

What do you mean, @Tas ? To solve the first problem by using the second? In any case, show please your attempts. — Michael Rozenberg, Apr 12 '20 at 19:56
@Tas I got $\measuredangle UFO=75^{\circ}.$ If you want to see my solution, show your attempts. — Michael Rozenberg, Apr 12 '20 at 20:16
@MichaelRozenberg I find a lot of angles and I got the equation $\angle UFO+\angle UFN=100°$, but I couldn't find the value of $\angle UFN$. Please, can you post your solution? — Tas, Apr 12 '20 at 20:39
Please recall what you mean by "russian triangle" in this context (not the film...). For the classical problem (second figure), a reference : https://math.stackexchange.com/questions/6942/finding-an-angle-within-an-80-80-20-isosceles-triangle — Jean Marie, Apr 13 '20 at 08:56
Not an answer, but this might help. If $Q$ is $EFU$'s circumcentre, $\angle FQU=2\angle FEU=10^\circ$. It is sufficient to prove that $QOU$ is straight, whence $\angle QUF=85^\circ\implies\angle EUF=20^\circ$. — Rosie F, Apr 15 '20 at 15:16
Does this answer your question? Find angle UFO in the picture attached — Rosie F, Apr 21 '20 at 17:53

Michael Rozenberg · Accepted Answer · 2020-04-13T19:56:20.880

Let $OF\cap UE=\{D\}$ and $\measuredangle UFO=x$.

Thus, $\measuredangle DUF=95^{\circ}$ and since $$\frac{OD}{UD}\cdot\frac{UD}{FD}\cdot\frac{FD}{ED}\cdot\frac{ED}{OD}=1,$$ by law of sines we obtain: $$\frac{\sin65^{\circ}}{\sin20^{\circ}}\cdot\frac{\sin{x}}{\sin(95^{\circ}-x)}\cdot \frac{\sin5^{\circ}}{\sin80^{\circ}}\cdot \frac{\sin60^{\circ}}{\sin35^{\circ}}=1 $$ or $$\frac{\sin65^{\circ}\sin5^{\circ}\sin60^{\circ}}{\sin20^{\circ}\sin80^{\circ}\sin35^{\circ}}=\sin95^{\circ}\cot{x}-\cos95^{\circ}$$ or $$\frac{\sin65^{\circ}\sin5^{\circ}\sin60^{\circ}}{\sin20^{\circ}\sin80^{\circ}\sin35^{\circ}}-\sin5^{\circ}=\cos5^{\circ}\cot{x}$$ or $$\tan5^{\circ}\left(\frac{\sin65^{\circ}\sin60^{\circ}}{\sin20^{\circ}\sin80^{\circ}\sin35^{\circ}}-1\right)=\cot{x}.$$ We need to prove that: $$\tan5^{\circ}\left(\frac{\sin65^{\circ}\sin60^{\circ}}{\sin20^{\circ}\sin80^{\circ}\sin35^{\circ}}-1\right)=\tan15^{\circ}$$ or $$\frac{\sin65^{\circ}\sin60^{\circ}}{\sin20^{\circ}\sin80^{\circ}\sin35^{\circ}}-1=\frac{3-\tan^25^{\circ}}{1-3\tan^25^{\circ}}$$ or $$\frac{\sin65^{\circ}\sin60^{\circ}}{\sin20^{\circ}\sin80^{\circ}\sin35^{\circ}}=\frac{4-4\tan^25^{\circ}}{1-3\tan^25^{\circ}}$$ or $$\frac{\sin65^{\circ}\sin60^{\circ}}{\sin20^{\circ}\sin80^{\circ}\sin35^{\circ}}=\frac{8\cos10^{\circ}}{1+\cos10^{\circ}-3+3\cos10^{\circ}}$$ or $$\frac{\sin65^{\circ}\sin60^{\circ}}{\sin20^{\circ}\sin80^{\circ}\sin35^{\circ}}=\frac{2\cos10^{\circ}}{\cos10^{\circ}-\cos60^{\circ}}$$ or $$\frac{\cos25^{\circ}\sin60^{\circ}}{\sin20^{\circ}\cos10^{\circ}\sin35^{\circ}}=\frac{\cos10^{\circ}}{\sin25^{\circ}\sin35^{\circ}}$$ or $$\sin50^{\circ}\sin60^{\circ}=\sin20^{\circ}(1+\cos20^{\circ})$$ or $$\sin60^{\circ}\cos40^{\circ}-\cos60^{\circ}\sin40^{\circ}=\sin20^{\circ},$$ which is obvious.

Oh! Nice answer! But, how do you solve this trigonometric equation? I wrote $$\frac{2\cos35°-\sqrt2}{16}=\sin95°\cot x-\cos95°$$. How can I solve this? — Tas, Apr 13 '20 at 17:37
@Tas If you can use a calculator, so just calculate $\arctan$. I am ready to show that $75^{\circ}$ is an unique root of the equation without calculator. — Michael Rozenberg, Apr 13 '20 at 17:41
I want to see this without calculator. If you can, thank you! — Tas, Apr 13 '20 at 18:02
@Tas I posted. Your second problem we can solve by the similar way. — Michael Rozenberg, Apr 13 '20 at 19:58

Solve for the angle UFO with the russian triangle

1 Answers1